利用三角函数线证明：
【难度】
【出处】
无
【标注】
-
若 $\alpha$ 为锐角，则 $\sin \alpha<\alpha<\tan \alpha$；标注答案略解析在单位圆中，画出 $\alpha$．
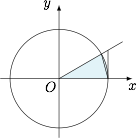因为扇形面积在两个三角形面积之间，所以$$\sin \alpha<\alpha<\tan \alpha.$$ -
若 $0<\alpha<\beta<\gamma<\dfrac{\pi}2$，则 $\dfrac{\pi}{2}+2\sin \alpha\cos \beta+2\sin \beta\cos \gamma>\sin 2\alpha+\sin 2\beta+\sin 2\gamma$．标注答案略解析如图，$3$ 条线分别代表 $\alpha$，$\beta$，$\gamma$ 的终边．
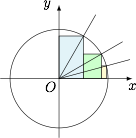因为四分之一圆的面积大于三个小矩形的面积之和，所以$$\begin{split}\dfrac {\pi}{4}&>\sin \gamma\cos \gamma+\sin \beta(\cos \beta-\cos \gamma)+\sin \alpha(\cos \alpha-\cos \beta)\\&=\dfrac 12\sin \gamma+\dfrac 12\sin \beta+\dfrac 12\sin \alpha-\sin \beta\cos \gamma-\sin \alpha\cos \beta,\end{split}$$即$$\dfrac{\pi}{2}+2\sin \alpha\cos \beta+2\sin \beta\cos \gamma>\sin 2\alpha+\sin 2\beta+\sin 2\gamma.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
