在四边形 $ABCD$ 中,对角线 $AC$,$BD$ 相交于点 $O$,将 $\triangle COD$ 绕点 $O$ 按逆时针方向旋转得到 $\triangle C_{1}OD_{1}$,旋转角为 $\theta\left(0^\circ <\theta <90^\circ \right)$,连接 $AC_{1}$,$BD _{1}$,$AC_{1}$ 与 $BD_{1}$ 交于点 $P$.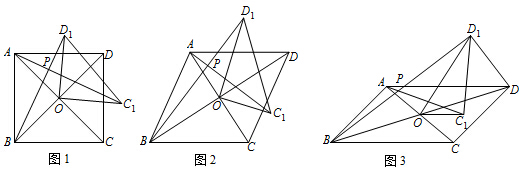

【难度】
【出处】
无
【标注】
-
如图1,若四边形 $ABCD$ 是正方形.
① 求证:$\triangle AOC _{1}\cong \triangle BOD _{1}$.
② 请直接写出 $AC_{1}$ 与 $BD_{1}$ 的位置关系.标注答案① 略;
② $AC_{1}\perp BD_{1}$解析① 因为四边形 $ABCD$ 是正方形,
所以 $ AC=BD$,$OC=OA= \dfrac{1}{2} AC$,$OD=OB= \dfrac{1}{2} BD $,
所以 $OC=OA=OD=OB$.
因为 $ \triangle C_{1}OD_{1}$ 由 $\triangle COD$ 绕点 $O$ 旋转得到,
所以 $ OC_{1}= OC$,$OD_{1}=OD$,$\angle COC_{1}=\angle DOD_{1}$,
所以 $ OC_{1}= OD_{1 }$,$\angle AOC_{1}=\angle BOD_{1}$,
所以 $ \triangle AOC_{1}\cong \triangle BOD_{1} $.
② $AC_{1}\perp BD_{1}$. -
如图 2,若四边形 $ABCD$ 是菱形,$AC=5$,$BD=7$,设 $AC_{1}=k BD_{1}$.判断 $AC_{1}$ 与 $BD_{1}$ 的位置关系,说明理由,并求出 $k$ 的值.标注答案$AC_{1}\perp BD_{1}$解析因为四边形 $ABCD$ 是菱形,
所以 $OC=OA=\dfrac{1}{2}AC$,$OD=OB=\dfrac{1}{2}BD$,$AC\perp BD$.
因为 $ \triangle C_{1}OD_{1}$ 由 $\triangle COD$ 绕点 $O$ 旋转得到,
所以 $ OC_{1}= OC$,$OD_{1}=OD$,$\angle COC_{1}=\angle DOD_{1} $,
所以 $OC_{1}=OA$,$OD_{1}=OB$,$\angle AOC_{1}=\angle BOD_{1}$,
所以 $ \dfrac{{O{C_1}}}{OA} = \dfrac{{O{D_1}}}{OB} $,
所以 $ \dfrac{{O{C_1}}}{{O{D_1}}} = \dfrac{OA}{OB}$,
所以 $\triangle AOC_{1}\backsim \triangle BOD_{1}$,
所以 $ \angle OAC_{1}= \angle OBD_{1}$.
又 $\angle AOB=90^\circ $,
所以 $ \angle OAB+\angle ABP+\angle OBD_{1}=90^\circ $,
所以 $\angle OAB+\angle ABP+\angle OAC_{1}=90^\circ $,
所以 $ \angle APB=90^\circ $,$ AC_{1}\perp BD_{1}$.
因为 $ \triangle AOC_{1}\backsim \triangle BOD_{1}$,
所以 $ \dfrac{{A{C_1}}}{{B{D_1}}} = \dfrac{OA}{OB} = \dfrac{{\dfrac{1}{2}AC}}{{\dfrac{1}{2}BD}} = \dfrac{AC}{BD} = \dfrac{5}{7}$,
所以 $ k = \dfrac{5}{7}$. -
如图 3,若四边形 $ABCD$ 是平行四边形,$AC=5$,$BD=10$,连接 $DD_{1}$,设 $AC_{1}=kBD_{1}$.请直接写出 $k$ 的值和 $AC_1^2+\left(kDD_1\right)^2$ 的值.标注答案$k = \dfrac{1}{2}$;$AC_1^2 + {\left(kD{D_1}\right)^2} = 25$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3