已知抛物线 $y=ax^2+x+c$（$a\neq 0$）经过 $A\left(-1,0\right)$，$B\left(2,0\right)$ 两点，与 $y$ 轴相交于点 $C$，该抛物线的顶点为点 $M$，对称轴与 $BC$ 相交于点 $N$，与 $x$ 轴交于点 $D$．
【难度】
【出处】
无
【标注】
-
求该抛物线的解析式及点 $M$ 的坐标；标注答案抛物线为 $y=-x^2+x+2=-\left(x-\dfrac12\right)^2+\dfrac94$，
顶点 $M\left(\dfrac12,\dfrac94\right)$解析因为抛物线 $y=ax^2+x+c$（$a\neq 0$）经过 $A\left(-1,0\right)$，$B\left(2,0\right)$ 两点，
所以 $\begin{cases}a-1+c=0,\\4a+2+c=0,\end{cases}$
解得 $\begin{cases}a=-1,\\c=2.\end{cases}$
所以抛物线为 $y=-x^2+x+2$；
所以抛物线为 $y=-x^2+x+2=-\left(x-\dfrac12\right)^2+\dfrac94$，
所以顶点 $M\left(\dfrac12,\dfrac94\right)$． -
点 $E$ 是该抛物线上一动点，且位于第一象限，当点 $E$ 到直线 $BC$ 的距离为 $\dfrac{\sqrt2}{2}$ 时，求点 $E$ 的坐标．标注答案$ E\left(1,2\right)$解析如图，作 $EF\perp BC$ 于 $F$，
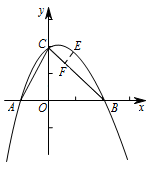因为直线 $BC$ 为 $y=-x+2$，
所以设 $E\left(m,-m^2+m+2\right)$，直线 $EF$ 为 $y=x+\left(-m^2+2\right)$，
解 $\begin{cases}y=-x+2,\\y=x+\left(-m^2+2\right),\end{cases}$ 得 $\begin{cases}x=\dfrac12m^2,\\y=-\dfrac12m^2+2,\end{cases}$
所以 $F\left(\dfrac 12m^2,-\dfrac 12m^2+2\right)$．
因为 $EF= \dfrac{\sqrt2}{2}$，
所以 $ \left(m-\dfrac 12 m^2\right)^2+\left(-\dfrac 12m^2+2+m^2-m-2\right)^2=\left(\dfrac{\sqrt2}{2} \right)^2$，解得 $m=1$，
所以 $ -m^2+m+2=2$，
所以 $E\left(1,2\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
