在平面直角坐标系中，$ O $ 为原点，点 $ A\left(-2,0\right) $，点 $ B\left(0,2\right) $，点 $ E $、点 $ F $ 分别为 $ OA $，$ OB $ 的中点．若正方形 $ OEDF $ 绕点 $ O $ 顺时针旋转，得正方形 $ OE'D'F' $，记旋转角为 $ {\alpha} $．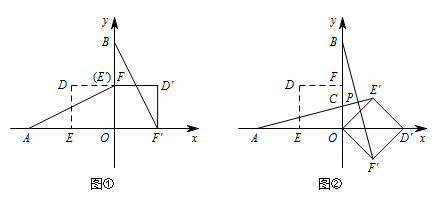
【难度】
【出处】
无
【标注】
-
如图 ①，当 $ {\alpha} =90^\circ $，求 $AE'$，$BF'$ 的长；标注答案$ AE' $，$ BF' $ 的长都等于 $ \sqrt5 $解析当 $ {\alpha} =90^\circ $ 时，点 $ E' $ 与点 $ F $ 重合，如图 ①．
因为点 $ A\left(-2,0\right) $ 点 $ B\left(0,2\right) $，
所以 $ OA=OB=2 $．
因为点 $ E $，点 $ F $ 分别为 $ OA $，$ OB $ 的中点，
所以 $ OE=OF=1 $
因为 正方形 $ OE'D'F'$ 是正方形 $ OEDF $ 绕点 $ O $ 顺时针旋转 $ 90^\circ $ 得到的，
所以 $ OE'=OE=1 $，$ OF'=OF=1 $．
在 ${\mathrm{ \mathrm {Rt}}}\triangle AE'O $ 中，$ AE'= \sqrt{OA^2+OE^2} ＝ \sqrt{2^2+1^2 }＝\sqrt 5 $．
在 $ {\mathrm{Rt}}\triangle BOF' $ 中，$ BF'= \sqrt{OB^2+OF^2 }＝\sqrt{ 2^2+1^2} ＝\sqrt 5 $．
所以 $ AE' $，$ BF' $ 的长都等于 $ \sqrt5 $． -
如图 ②，当 $ {\alpha} =135^\circ $，求证 $AE'=BF'$，且 $AE' \perp BF'$；标注答案略解析当 $ {\alpha} =135^\circ $ 时，如图 ②．
因为正方形 $ OE'D'F' $ 是由正方形 $ OEDF $ 绕点 $ O $ 顺时针旋转 $ 135^\circ $ 所得，
所以 $ \angle AOE'=\angle BOF'=135^\circ $．
在 $ \triangle AOE' $ 和 $ \triangle BOF'$ 中，$ AO＝BO $，$ \angle AOE'＝\angle BOF' $，$ OE'＝OF' $，
所以 $ \triangle AOE'\cong \triangle BOF' $（${\mathrm{SAS}}$）．
所以 $ AE'=BF' $，且 $ \angle OAE'=\angle OBF' $．
因为 $ \angle ACB=\angle CAO+\angle AOC=\angle CBP+\angle CPB$，$\angle CAO=\angle CBP $，
所以 $ \angle CPB=\angle AOC=90^\circ $，
所以 $ AE'\perp BF' $． -
若直线 $AE'$ 与直线 $BF'$ 相交于点 $P$，求点 $P$ 的纵坐标的最大值（直接写出结果即可）．标注答案点 $ P $ 的纵坐标的最大值为 $ \dfrac{\sqrt 3 +1} 2 $解析在第一象限内，当点 $ D'$ 与点 $ P $ 重合时，点 $ P $ 的纵坐标最大．
过点 $ P $ 作 $ PH\perp x $ 轴，垂足为 $ H $，如图所示．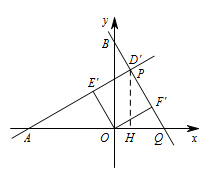
因为 $ \angle AE'O=90^\circ $，$ E'O=1 $，$ AO=2 $，
所以 $ \angle E'AO=30^\circ $，$ AE'=\sqrt 3 $．
所以 $ AP=\sqrt 3 +1 $．
因为 $ \angle AHP=90^\circ $，$ \angle PAH=30^\circ $，
所以 $ PH=\dfrac1 2 AP=\dfrac{\sqrt3 +1 }2 $．
所以点 $ P $ 的纵坐标的最大值为 $ \dfrac{\sqrt 3 +1} 2 $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
