如图，已知圆 $G:(x-2)^2+y^2=r^2$ 是椭圆 $\dfrac{x^2}{16}+y^2=1$ 的内接 $\triangle ABC$ 的内切圆，其中 $A$ 为椭圆的左顶点．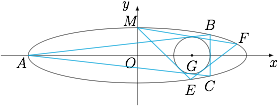
【难度】
【出处】
无
【标注】
-
求圆 $G$ 的半径 $r$；标注答案$\dfrac 23$解析如图，设切点分别为 $P,Q$．
由 $\triangle APG$ 与 $\triangle AQB$ 相似，有$$\frac{PG}{AP}=\frac{BQ}{AQ},$$于是$$\frac{r}{\sqrt{36-r^2}}=\frac{BQ}{6+r},$$从而$$BQ=r\cdot\sqrt{\frac{6+r}{6-r}}.$$将 $B$ 的坐标代入椭圆方程有$$\frac{1}{16}\cdot (2+r)^2+\left(r\cdot\sqrt{\frac{6+r}{6-r}}\right)^2=1,$$注意到 $r=-6$ 是该方程的一个解，解得正根 $r=\dfrac 23$． -
过 $M(0,1)$ 作圆的两条切线交椭圆于 $E,F$ 两点，证明：直线 $EF$ 与圆 $G$ 相切．标注答案略解析设过 $M$ 的切线为 $y=kx+1$，则由直线与圆的位置关系可得$$\dfrac{\left|2k+1\right|}{\sqrt{1+k^2}}=\dfrac 23,$$即$$32k^2+36k+5=0.$$于是设直线 $ME,MF$ 的斜率分别为 $k_1,k_2$，则$$k_1+k_2=-\dfrac{9}{8},k_1\cdot k_2=\dfrac 5{32}.$$将两条相交直线 $ME\cup MF$ 看作是一条曲线$$\left(y-k_1x-1\right)\cdot\left(y-k_2x-1\right)=0,$$注意到这条曲线与椭圆的交点为 $M,E,F$，因此需要设法联立变形为直线方程，且在联立过程中去掉解 $x=0,y=1$．于是将该曲线方程和椭圆方程分别变形为$$-k_1\cdot k_2x^2=(y-1)^2-(k_1+k_2)x(y-1)$$和$$-\frac 1{16}x^2=y^2-1,$$将 $k_1+k_2$ 和 $k_1\cdot k_2$ 代入，两式相比得$$\dfrac 52=\dfrac{y-1+\dfrac 98x}{y+1},$$化简得$$EF:9x-12y-28=0.$$从而圆心 $G(2,0)$ 到直线 $EF$ 的距离为$$\dfrac{10}{\sqrt{9^2+12^2}}=\dfrac 23=r,$$原命题得证．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
