已知不共面的直线 $a,b,c$ 相交于 $O$ 点,$M,P$ 是直线 $a$ 上两点,$N,Q$ 分别是 $b,c$ 上两点,求证:$MN$ 和 $PQ$ 是异面直线.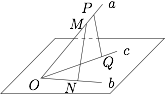

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
若 $MN$ 与 $PQ$ 共面 $\alpha$,那么对平面 $\alpha,POQ,MON$ 应用透视原理即可推出直线 $a,MN,PQ$ 交于一点,但 $P\ne M$,矛盾.因此 $MN$ 与 $PQ$ 是异面直线.
答案
解析
备注