查看数据源：597ea54bd05b90000b5e315e
已知 $a,b,c$ 是空间中的三条不同的直线，讨论与 $a,b,c$ 都相交的直线条数．
【难度】
【出处】
无
【标注】
  • 知识点
    >
    立体几何
    >
    空间位置关系
    >
    平面的基本性质
【答案】
略
【解析】
情形 1 $a,b,c$ 中存在共面的两条直线．不妨设设共面的两条直线为 $a,b$，它们确定的平面为 $\alpha$．
情形 1-1 $c\subset \alpha$．此时显然平面 $\alpha$ 内任意一条与 $a,b,c$ 均不平行的直线即符合题意，有无数条；
情形 1-2 $c\cap \alpha=P$．此时平面 $\alpha$ 内过 $P$ 且与直线 $a,b$ 均不平行的直线即符合题意，有无数条；
情形1-3 $c\parallel \alpha$．此时若 $a\cap b=P$，那么连接直线 $c$ 上任意一点 $Q$ 与点 $P$ 所得到的直线即符合题意；若 $a\parallel b$，那么与 $a,b$ 均相交的直线必然在平面 $\alpha$ 内，又 $c\parallel \alpha$，因此不存在符合题意的直线．
情形 2 $a,b,c$ 两两异面．在直线 $a$ 上任取点 $A$，设点 $A$ 与直线 $c$ 确定的平面为 $\alpha_A$，那么这样的平面有无数个，且这些平面都交于直线 $c$．与直线 $b$ 相交的平面 $\alpha(A)$ 有无数个，这是因为直线 $b$ 至多和这些平面中的一个平行，否则假设 $b$ 与 $\alpha_{A_1}$ 和 $\alpha_{A_2}$ 均平行，那么 $b$ 和 $A_1,A_2$ 所确定的平面与 $\alpha_{A_1},\alpha_{A_2}$ 的交线 $l_1,l_2$ 均与 $b$ 平行．考虑 $l_1,l_2$ 形成的平面与平面 $\alpha_{A_1},\alpha_{A_2}$，根据透视原理，它们两两的交线两两平行，于是 $b\parallel c$，矛盾．设直线 $b$ 与平面 $\alpha_A$ 相交于点 $B_A$，考虑直线 $AB_A$，当 $A$ 变化时一系列直线 $AB_A$ 中至多只有一条与 $c$ 平行，否则 $A_1B_{A_1}\parallel A_2B_{A_2}\parallel c$，于是 $A_1,B_{A_1},A_2,B_{A_2}$ 四点共面，进而 $a,b$ 共面，矛盾．这样就构造出了无数条符合题意的直线 $AB_A$．
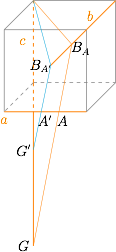
以立方体中三条两两异面的棱为例，配示意图如下：
答案 解析 备注
0.118735s