已知椭圆 $\dfrac{x^2}{4}+\dfrac{y^2}{3}=1$ 上的两点 $A,B$ 关于 $x$ 轴对称，$P(4,0)$ 是椭圆长轴所在直线上的一定点，设直线 $PB$ 与椭圆相交于 $D$，证明：直线 $AD$ 恒过定点，并求定点坐标．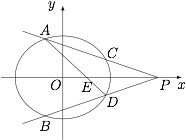
【难度】
【出处】
无
【标注】
【答案】
$(1,0)$
【解析】
将椭圆通过伸缩变换为圆，则需证明：
引理 若点 $A,B$ 为关于圆的直径 $HG$ 对称的两点，$HG$ 所在直线上的一点 $P$ 与 $B$ 点的连线交圆于 $D$，则 $AD$ 与 $PH$ 交于定点 $E$．
证明 如图，连接 $AG,GD$，设 $PA$ 与圆交于 $C$．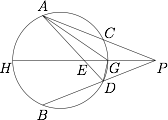
因为 $G$ 为弧 $CD$ 和弧 $AB$ 的中点，所以 $AG,DH$ 分别是 $\angle{A}$ 和 $\angle{BDG}$ 的平分线，而 $DG\perp DH$，所以 $DG$ 是 $\angle{EDP}$ 的平分线．于是$$\dfrac{AE}{AP}=\dfrac{DE}{DP}=\dfrac{EG}{GP},$$因此$$\dfrac{AE\cdot DE}{AP\cdot DP}=\left(\dfrac{EG}{GP}\right),$$而 $AE\cdot DE=EG\cdot EH$（相交弦定理），$AP\cdot DP=AP\cdot CP=PG\cdot PH$（切割线定理），于是$$\dfrac{EG\cdot EH}{PG\cdot PH}=\dfrac{EG}{PG}\cdot \dfrac{EG}{PG},$$即$$\dfrac{EG}{EH}=\dfrac{PG}{PH}.$$因为 $\dfrac{PG}{PH}$ 为定值（在本例中为 $\dfrac 13$），所以 $\dfrac{EG}{EH}$ 为定值，$E$ 为定点（在本例中 $E(1,0)$）．
因为 $G$ 为弧 $CD$ 和弧 $AB$ 的中点，所以 $AG,DH$ 分别是 $\angle{A}$ 和 $\angle{BDG}$ 的平分线，而 $DG\perp DH$，所以 $DG$ 是 $\angle{EDP}$ 的平分线．于是$$\dfrac{AE}{AP}=\dfrac{DE}{DP}=\dfrac{EG}{GP},$$因此$$\dfrac{AE\cdot DE}{AP\cdot DP}=\left(\dfrac{EG}{GP}\right),$$而 $AE\cdot DE=EG\cdot EH$（相交弦定理），$AP\cdot DP=AP\cdot CP=PG\cdot PH$（切割线定理），于是$$\dfrac{EG\cdot EH}{PG\cdot PH}=\dfrac{EG}{PG}\cdot \dfrac{EG}{PG},$$即$$\dfrac{EG}{EH}=\dfrac{PG}{PH}.$$因为 $\dfrac{PG}{PH}$ 为定值（在本例中为 $\dfrac 13$），所以 $\dfrac{EG}{EH}$ 为定值，$E$ 为定点（在本例中 $E(1,0)$）．
答案
解析
备注
