已知直角 $\triangle OAB$ 的斜边端点 $A,B$ 均在椭圆 $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ 上,$O$ 为坐标原点,求证:$\triangle OAB$ 斜边上的高为定值.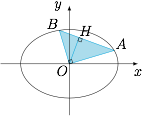

【难度】
【出处】
无
【标注】
【答案】
$\dfrac{ab}{\sqrt{a^2+b^2}}$
【解析】
不妨设 $A(\theta:r_1)$,$B\left(\theta+\dfrac{\pi}2:r_2\right)$,于是\[\begin{cases}\dfrac{r_1^2\cos^2\theta}{a^2}+\dfrac{r_1^2\sin^2\theta}{b^2}=1,\\ \dfrac{r_2^2\cos^2\left(\theta+\dfrac{\pi}2\right)}{a^2}+\dfrac{r_2^2\sin^2\left(\theta+\dfrac{\pi}2\right)}{b^2}=1,\end{cases}\]于是 $\triangle OAB$ 斜边上的高 $h$ 满足\[\dfrac{1}{h^2}=\dfrac{1}{r_1^2}+\dfrac{1}{r_2^2}=\dfrac 1{a^2}+\dfrac 1{b^2}\]为定值,因此 $h$ 为定值 $\dfrac{ab}{\sqrt{a^2+b^2}}$.
答案
解析
备注