已知抛物线 $C:y^2=2px$ 的焦点为 $F$,$A$ 为抛物线上一点,$D$ 为 $x$ 轴正半轴上一点,且 $|FA|=|FD|$,直线 $AD$ 交抛物线于另一点 $B$.抛物线在 $E$ 点处的切线与直线 $AB$ 平行.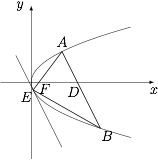

【难度】
【出处】
无
【标注】
-
求证:直线 $AE$ 恒过定点;标注答案略解析设 $A(2pa^2,2pa)$,$B(2pb^2,2pb)$,则根据抛物线的平均性质,有 $D$ 点的横坐标\[p+2pa^2=-2pab,\]即\[a+b=-\dfrac 1{2a}.\]根据抛物线的平均性质有 $E$ 点的纵坐标为 $p(a+b)$,于是 $E$ 点的横坐标为 $\dfrac{p(a+b)^2}{2}$,再根据抛物线的平均性质,可得直线 $AE$ 的横截距为\[\sqrt{\dfrac{p(a+b)^2}2\cdot 2pa^2}=-pa(a+b)=\dfrac p2,\]因此直线 $AE$ 恒过点 $F\left(\dfrac p2,0\right)$.
-
求 $\triangle EAB$ 的面积的最小值.标注答案$8p^3$解析$E$ 点坐标 $\left(\dfrac{p(a+b)^2}2,p(a+b)\right)$,$A(2pa^2,2pa)$,$B(2pb^2,2pb)$,于是根据三角形面积坐标公式,可得 $\triangle EAB$ 的有向面积\[\begin{split}
\overrightarrow{S}&=\begin{vmatrix}2pa^2-\dfrac{p(a+b)^2}2& 2pa-p(a+b) \\
2pb^2-\dfrac{p(a+b)^2}2 & 2pb-p(a+b)
\end{vmatrix}\\
&=p^2(a-b) \cdot \begin{vmatrix} 2a^2-\dfrac{(a+b)^2}2 & 1 \\ 2b^2-\dfrac{(a+b)^2}2 & -1 \end{vmatrix},
\end{split}\]于是 $\triangle EAB$ 的面积\[\begin{split}S&=p^2\cdot |a-b|\cdot \left|2(a^2+b^2)-(a+b)^2\right|\\
&=p^2\cdot |a-b|^3\\
&=p^2\cdot \left|2a+\dfrac{1}{2a}\right|^3\\
&\geqslant 8p^2,
\end{split}\]等号当 $a=\pm \dfrac 12$ 时取得.因此所求面积的最小值为 $8p^3$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2