已知某椭圆的焦点是 $F_1(-4,0)$,$F_2(4,0)$,过点 $F_1$ 并垂直于 $x$ 轴的直线与椭圆的一个交点为 $B$,且 $|F_1B|+|F_2B|=10$.椭圆上不同的两点 $A(x_1,y_1)$,$C(x_2,y_2)$ 满足条件:$|F_2A|,|F_2B|,|F_2C|$ 成等差数列.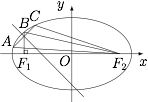

【难度】
【出处】
无
【标注】
-
求该椭圆的方程;标注答案$\dfrac {x^2}{25}+\dfrac {y^2}9=1$解析略
-
求弦 $AC$ 中点的横坐标;标注答案$-4$解析根据焦半径公式,弦 $AC$ 中点 $M$ 的横坐标与点 $B$ 点的坐标相等,为 $-4$;
-
设弦 $AC$ 的垂直平分线的方程为 $y=kx+m$,求 $m$ 的取值范围.标注答案$\left(-\dfrac {16}5,\dfrac {16}5\right)$解析由椭圆的垂径定理,得 $k_{AC}\cdot k_{OM} = - \dfrac {b^2}{a^2}=-\dfrac 9{25}$,根据题意又有 $k\cdot k_{AC}=-1$.两式相除,得$$k=\dfrac {25}9 \cdot k_{OM} = \dfrac {25y_0}{36}.$$另一方面,由于 $M$ 在弦 $AC$ 的垂直平分线上,于是 $m=y_0-4k=-\dfrac {16y_0}9$.因为 $y_0$ 的取值范围为 $\left(-\dfrac 95,\dfrac 95\right)$,因此 $m$ 的取值范围是 $\left(-\dfrac {16}5,\dfrac {16}5\right)$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3