已知 $F_1,F_2$ 分别是双曲线 $C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$($a>b>0$)的左、右焦点,$B$ 是虚轴的端点,直线 $F_1B$ 与 $C$ 的两条渐近线分别交于 $P,Q$ 两点,线段 $PQ$ 的垂直平分线与 $x$ 轴交于点 $M$.若 $|MF_2|=|F_1F_2|$,求 $C$ 的离心率.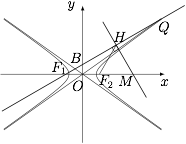

【难度】
【出处】
2012年高考浙江卷(理)
【标注】
【答案】
$\dfrac{\sqrt 6}2$
【解析】
应用双曲线的渐近线的“垂径定理”.
设 $H(m,n)$,双曲线的半焦距为 $c$,则\[\begin{cases}\dfrac{n}{m+c}=\dfrac bc,\\ \dfrac nm\cdot \dfrac bc=\dfrac {b^2}{a^2},\\ \dfrac{n}{m-3c}\cdot \dfrac bc=-1,\end{cases}\]分别用第一个方程和第三个方程除第一个方程,可得\[\dfrac cm=\dfrac{b^2}{a^2}=\dfrac{c^2}{3a^2},\]于是解得 $e=\dfrac{\sqrt 6}2$.
设 $H(m,n)$,双曲线的半焦距为 $c$,则\[\begin{cases}\dfrac{n}{m+c}=\dfrac bc,\\ \dfrac nm\cdot \dfrac bc=\dfrac {b^2}{a^2},\\ \dfrac{n}{m-3c}\cdot \dfrac bc=-1,\end{cases}\]分别用第一个方程和第三个方程除第一个方程,可得\[\dfrac cm=\dfrac{b^2}{a^2}=\dfrac{c^2}{3a^2},\]于是解得 $e=\dfrac{\sqrt 6}2$.
答案
解析
备注