求平面内与两定点 $A(-a,0)$、$B(a,0)(a>0)$ 连线的斜率之积等于非零常数 $m$ 的点的轨迹.
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设动点的坐标为 $(x,y)$,那么\[\dfrac{y}{x+a}\cdot \dfrac{y}{x-a}=m,\]$y^{2}=m(x^{2}-a^{2})$,$mx^{2}-y^{2}=ma^{2}$,$\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{ma^{2}}=1$.
当 $m>0$,曲线 $C$ 是焦点在 $x$ 轴上的双曲线,离心率为 $\sqrt{1+m}$;
当 $-1<m<0$ 时,曲线 $C$ 是焦点在 $x$ 上的椭圆,离心率为 $\sqrt{1+m}$;
当 $m=-1$ 时,曲线 $C$ 是圆;
当 $m<-1$ 时,曲线 $C$ 是焦点在 $y$ 轴上的椭圆,离心率为 $\sqrt{1+\dfrac{1}{m}}$.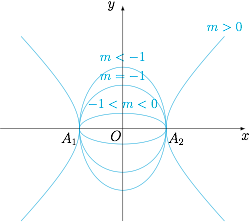
当 $m>0$,曲线 $C$ 是焦点在 $x$ 轴上的双曲线,离心率为 $\sqrt{1+m}$;
当 $-1<m<0$ 时,曲线 $C$ 是焦点在 $x$ 上的椭圆,离心率为 $\sqrt{1+m}$;
当 $m=-1$ 时,曲线 $C$ 是圆;
当 $m<-1$ 时,曲线 $C$ 是焦点在 $y$ 轴上的椭圆,离心率为 $\sqrt{1+\dfrac{1}{m}}$.

答案
解析
备注