已知两条直线 $l_1,l_2$ 相交于点 $O$，点 $A$ 在直线 $l_1$ 上运动，点 $B$ 在直线 $l_2$ 上运动，且 $\triangle AOB$ 的面积为定值 $S$，求 $AB$ 的中点 $M$ 的轨迹．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图建系，设 $l_1,l_2$ 的夹角为 $2\theta$，$k=\tan\theta$，直线 $OA$ 和直线 $OB$ 的方程分别为 $y=kx$ 和 $y=-kx$．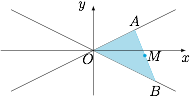
设 $A(a,ka)$，$B(b,-kb)$，$M(x,y)$，根据题意，有\[S=\dfrac 12\sin 2\theta\cdot \left(\sqrt{1+k^2}\cdot |a|\right)\cdot\left(\sqrt{1+k^2}\cdot |b|\right)=k|ab|,\]又\[2x=a+b,2y=k(a-b),\]代入\[(a+b)^2-(a-b)^2=4ab,\]中，可得\[kx^2-\dfrac{y^2}k=\pm S.\]
设 $A(a,ka)$，$B(b,-kb)$，$M(x,y)$，根据题意，有\[S=\dfrac 12\sin 2\theta\cdot \left(\sqrt{1+k^2}\cdot |a|\right)\cdot\left(\sqrt{1+k^2}\cdot |b|\right)=k|ab|,\]又\[2x=a+b,2y=k(a-b),\]代入\[(a+b)^2-(a-b)^2=4ab,\]中，可得\[kx^2-\dfrac{y^2}k=\pm S.\]
答案
解析
备注
