在平面直角坐标系 $xOy$ 中，纵横坐标都是整数的点称为整点，顶点均为整点的多边形称为整点多边形，下列说法正确的是 \((\qquad)\)
【难度】
【出处】
2017年清华大学THUSSAT附加学科测试数学部分（二测）
【标注】
【答案】
BD
【解析】
可以证明整点正 $n$ 边形只有一种，为正方形．
容易证明不存在整点正三角形，因为边长平方是整数的正三角形面积为无理数，而格点多边形的面积为有理数．而整点正方形显然存在．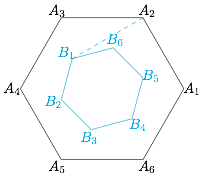
假设存在整点正 $n$ 边形，其中 $n\geqslant 5$，则必然存在边长最小的一个，设为 $A_1A_2\cdots A_n$．显然任何一个整点绕另外一个整点旋转 $90^\circ$ 后仍然为整点．由于正 $n$ 边形 $A_1A_2\cdots A_n$ 的内角为钝角，于是可以将 $A_i$ 绕 $A_{i+1}$ 向正 $n$ 边形内侧旋转 $90^\circ$ 得到 $B_i$（其中角标均在模 $n$ 的意义下），其中 $i=1,2,\cdots,n$．此时多边形 $B_1B_2\cdots B_n$ 也为整点正 $n$ 边形，但它的边长比 $A_1A_2\cdots A_n$ 小，矛盾．
综上所述，整点正 $n$ 边形只有一种，为正方形．选项 AC 错误，选项 BD 正确．
容易证明不存在整点正三角形，因为边长平方是整数的正三角形面积为无理数，而格点多边形的面积为有理数．而整点正方形显然存在．
假设存在整点正 $n$ 边形，其中 $n\geqslant 5$，则必然存在边长最小的一个，设为 $A_1A_2\cdots A_n$．显然任何一个整点绕另外一个整点旋转 $90^\circ$ 后仍然为整点．由于正 $n$ 边形 $A_1A_2\cdots A_n$ 的内角为钝角，于是可以将 $A_i$ 绕 $A_{i+1}$ 向正 $n$ 边形内侧旋转 $90^\circ$ 得到 $B_i$（其中角标均在模 $n$ 的意义下），其中 $i=1,2,\cdots,n$．此时多边形 $B_1B_2\cdots B_n$ 也为整点正 $n$ 边形，但它的边长比 $A_1A_2\cdots A_n$ 小，矛盾．综上所述，整点正 $n$ 边形只有一种，为正方形．选项 AC 错误，选项 BD 正确．
题目
答案
解析
备注
