查看数据源：597e8f17d05b900009165101
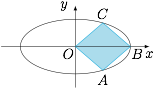
已知 $A,B,C$ 是椭圆 $E:\dfrac{x^2}4+y^2=1$ 上的三个点，$O$ 为坐标原点．
【难度】
【出处】
2013年高考北京卷（理）
【标注】
  • 知识点
    >
    解析几何
    >
    椭圆
    >
    椭圆的几何量
    >
    椭圆的基本量
  • 题型
    >
    解析几何
    >
    圆锥曲线的性质证明问题
  • 知识点
    >
    解析几何
    >
    椭圆
    >
    椭圆的性质
    >
    椭圆的垂径定理
  1. 当 $B$ 是 $E$ 的右顶点，且四边形 $OABC$ 为菱形时，求此菱形的面积；
    标注
    • 知识点
      >
      解析几何
      >
      椭圆
      >
      椭圆的几何量
      >
      椭圆的基本量
    答案
    $\sqrt 3$
    解析
    菱形的面积为 $\sqrt 3$．
  2. 当点 $B$ 不是 $E$ 的顶点时，判断四边形 $OABC$ 是否可能是菱形，并说明理由．
    标注
    • 题型
      >
      解析几何
      >
      圆锥曲线的性质证明问题
    • 知识点
      >
      解析几何
      >
      椭圆
      >
      椭圆的性质
      >
      椭圆的垂径定理
    答案
    略
    解析
    四边形 $OABC$ 不可能为菱形．用反证法证明如下：
    假设四边形 $OABC$ 是菱形．当点 $B$ 不是 $W$ 的顶点时，直线 $OB$ 和直线 $AC$ 的斜率都存在．菱形 $OABC$ 中 $OB$ 平分 $AC$，由椭圆的“垂径定理”得直线 $AC$ 与直线 $OB$ 的斜率之积为 $-\dfrac 14$，从而 $AC$ 与 $OB$ 不垂直，与四边形 $OABC$ 是菱形矛盾．
    因此四边形 $OABC$ 不可能为菱形．
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.108186s