已知椭圆 $C$ 的方程为 $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$($a > b > 0$),双曲线 $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$ 的两条渐近线为 ${l_1},{l_2}$,过椭圆 $C$ 的右焦点 $F$ 作直线 $l$,使 $l \perp {l_1}$,又 $l$ 与 ${l_2}$ 交于点 $P$,设 $l$ 与椭圆 $C$ 的两个交点从上至下依次是 $A,B$,求 $\dfrac{{\left| {FA} \right|}}{{\left| {AP} \right|}}$ 的最大值.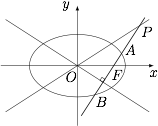

【难度】
【出处】
无
【标注】
【答案】
$\sqrt 2 - 1$
【解析】
直线 ${l_2}:y = \dfrac{b}{a}x$,直线 $AB:y = \dfrac{a}{b}\left( {x - c} \right)$,于是 ${x_P} = \dfrac{{{a^2}}}{c}$.注意到 $P$ 在右准线上,设 $A$ 到右准线的距离为 $d$,则 $\left| {AF} \right| = \dfrac{c}{a} \cdot d$,于是$$\dfrac{{\left| {AF} \right|}}{{\left| {AP} \right|}} = \dfrac{c}{a} \cdot \dfrac{d}{{\left| {AP} \right|}} = \dfrac{c}{a} \cdot \cos \theta,$$其中 $\theta = \angle AFx$,$\tan \theta = \dfrac{a}{b}$,于是\[\begin{split}\dfrac{|AF|}{|AP|}&= \dfrac{c}{a} \cdot \dfrac{b}{{\sqrt {{a^2} + {b^2}} }} = \sqrt {\dfrac{{\left( {{a^2} - {b^2}} \right){b^2}}}{{{a^2}\left( {{a^2} + {b^2}} \right)}}}
= \sqrt {\dfrac{{x - 1}}{{{x^2} + x}}}\\& = \sqrt {\dfrac{t}{{{{\left( {t + 1} \right)}^2} + \left( {t + 1} \right)}}} = \sqrt {\dfrac{1}{{t + \dfrac{2}{t} + 3}}} \\& \leqslant \sqrt {\dfrac{1}{{2\sqrt 2 + 3}}} = \sqrt 2 - 1, \end{split}\]其中 $x=\dfrac{a^2}{b^2}$,$t=x-1$,等号当且仅当 $t = \sqrt 2 $,$x = 1 + \sqrt 2 $,${a^2} = \left( {\sqrt 2 + 1} \right){b^2}$,即离心率为 $2 - \sqrt 2 $ 时取得.于是 $\dfrac{{\left| {FA} \right|}}{{\left| {AP} \right|}}$ 的最大值为 $\sqrt 2 - 1$.
= \sqrt {\dfrac{{x - 1}}{{{x^2} + x}}}\\& = \sqrt {\dfrac{t}{{{{\left( {t + 1} \right)}^2} + \left( {t + 1} \right)}}} = \sqrt {\dfrac{1}{{t + \dfrac{2}{t} + 3}}} \\& \leqslant \sqrt {\dfrac{1}{{2\sqrt 2 + 3}}} = \sqrt 2 - 1, \end{split}\]其中 $x=\dfrac{a^2}{b^2}$,$t=x-1$,等号当且仅当 $t = \sqrt 2 $,$x = 1 + \sqrt 2 $,${a^2} = \left( {\sqrt 2 + 1} \right){b^2}$,即离心率为 $2 - \sqrt 2 $ 时取得.于是 $\dfrac{{\left| {FA} \right|}}{{\left| {AP} \right|}}$ 的最大值为 $\sqrt 2 - 1$.
答案
解析
备注