长方体 $ABCD-A_1B_1C_1D_1$ 中,$AB=a$,$BC=b$,$BB_1=c$,并且 $a>b>c>0$.求沿着长方体的表面自 $A$ 到 $C_1$ 的最短线路的长.
【难度】
【出处】
无
【标注】
【答案】
$\sqrt{a^2+b^2+c^2+2bc}$
【解析】
如图.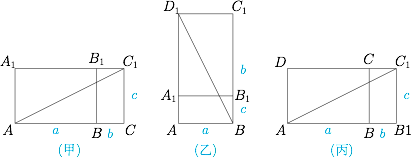

答案
解析
备注