已知 $a , b , c > 0$,$a + b + c = 1$,求证:$$2\sqrt 3 \leqslant \sqrt {3{a^2} + 1} + \sqrt {3{b^2} + 1} + \sqrt {3{c^2} + 1} < 4.$$
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
构造函数不等式$$\dfrac{{2\sqrt 3 }}{3} + \dfrac{{\sqrt 3 }}{2}\left( {x - \dfrac{1}{3}} \right)\leqslant \sqrt {3{x^2} + 1} \leqslant x+1.$$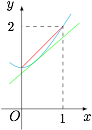

答案
解析
备注