已知 $M(x_0,y_0)$ 是双曲线 $C:\dfrac {x^2}{2}-y^2=1$ 上的一点，$F_1,F_2$ 是 $C$ 的两个焦点，若 $\overrightarrow {MF_1}\cdot \overrightarrow {MF_2}<0$，则 $y_0$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
2015年高考全国Ⅰ卷（理）
【标注】
【答案】
A
【解析】
考虑条件 $\overrightarrow{MF_1}\cdot\overrightarrow{MF_2}<0$ 边界情形为 $\overrightarrow{MF_1}\cdot \overrightarrow{MF_2}=0$，几何意义为点 $M$ 的轨迹是以 $F_1$、$F_2$ 为直径端点的圆．进而可知符合题意的点 $M$ 均在圆内，如图．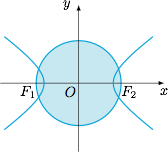
根据双曲线的焦点三角形面积公式，有$$S_{\triangle MF_1F_2}=1^2\cdot\cot{\dfrac{90^\circ}2}=1,$$另一方面，三角形 $MF_1F_2$ 的底 $F_1F_2$ 的长为 $2\sqrt 3$，于是可得其边 $F_1F_2$ 上的高为 $\dfrac{\sqrt 3}3$．
因此可得所求 $y_0$ 的取值范围是 $\left(-\dfrac{\sqrt 3}{3},\dfrac{\sqrt 3}{3}\right)$．
根据双曲线的焦点三角形面积公式，有$$S_{\triangle MF_1F_2}=1^2\cdot\cot{\dfrac{90^\circ}2}=1,$$另一方面，三角形 $MF_1F_2$ 的底 $F_1F_2$ 的长为 $2\sqrt 3$，于是可得其边 $F_1F_2$ 上的高为 $\dfrac{\sqrt 3}3$．因此可得所求 $y_0$ 的取值范围是 $\left(-\dfrac{\sqrt 3}{3},\dfrac{\sqrt 3}{3}\right)$．
题目
答案
解析
备注
