如图，在直三棱柱 $A_1B_1C_1-ABC$ 中，$\angle{BAC}=\dfrac{\pi}{2}$，$AB=AC=AA_1=2$，点 $G$ 与 $E$ 分别为线段 $A_1B_1$ 和 $C_1C$ 的中点，点 $D$ 与 $F$ 分别为线段 $AC$ 和 $AB$ 上的动点．若 $GD\perp EF$，则线段 $DF$ 长度的最小值是 \((\qquad)\) 
【难度】
【出处】
无
【标注】
【答案】
C
【解析】
如图建系．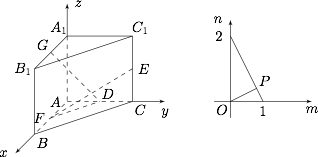
有 $A(0,0,0)$，$B(2,0,0)$，$C(0,2,0)$，$A_1(0,0,2)$，$B_1(2,0,2)$，$C_1(0,2,2)$，$D(0,m,0)$，$E(0,2,1)$，$F(n,0,0)$，$G(1,0,2)$，则$$0\leqslant m \leqslant 2,0\leqslant n\leqslant 2,$$因为 $\overrightarrow{GD}\cdot \overrightarrow{EF}=0$，所以$$(1,-m,2)\cdot(n,-2,-1)=0,$$即$$2m+n=2.$$此时 $|DF|=\sqrt{m^2+n^2}$，为连结点 $(1,0)$ 与 $(0,2)$ 的线段上的点 $P$ 到原点的距离 $OP$，显然当 $OP$ 与该线段垂直时，$|DF|$ 最小，为$$\dfrac{1\times 2}{\sqrt{1^2+2^2}}=\dfrac{2\sqrt 5}{5}.$$
有 $A(0,0,0)$，$B(2,0,0)$，$C(0,2,0)$，$A_1(0,0,2)$，$B_1(2,0,2)$，$C_1(0,2,2)$，$D(0,m,0)$，$E(0,2,1)$，$F(n,0,0)$，$G(1,0,2)$，则$$0\leqslant m \leqslant 2,0\leqslant n\leqslant 2,$$因为 $\overrightarrow{GD}\cdot \overrightarrow{EF}=0$，所以$$(1,-m,2)\cdot(n,-2,-1)=0,$$即$$2m+n=2.$$此时 $|DF|=\sqrt{m^2+n^2}$，为连结点 $(1,0)$ 与 $(0,2)$ 的线段上的点 $P$ 到原点的距离 $OP$，显然当 $OP$ 与该线段垂直时，$|DF|$ 最小，为$$\dfrac{1\times 2}{\sqrt{1^2+2^2}}=\dfrac{2\sqrt 5}{5}.$$
题目
答案
解析
备注
