设 ${x_1}>0$,${x_{n+1}}=\dfrac{{3\left( {1+{x_n}} \right)}}{{3+{x_n}}}$,$n=1 , 2 , 3 , \cdots $,判断数列 $\{x_n\}$ 的单调性.
【难度】
【出处】
无
【标注】
【答案】
当 $0<x_1<\sqrt 3$ 时,$\{x_n\}$ 单调递增;当 $x_1=\sqrt 3$ 时,$\{x_n\}$ 是常数列;当 $x_1>\sqrt 3$ 时,$\{x_n\}$ 单调递减
【解析】
如图.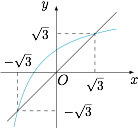

答案
解析
备注