有 $10$ 个同学，每天都有 $5$ 个人一起相约去看电影，他们都喜新厌旧，任意 $2$ 个人最多一起看两场电影（比如第一天 $5$ 个人中有韩梅梅和李雷，第二天里也有韩梅梅和李雷，那么之后韩梅梅和李雷就再也不会一起看电影了），$10$ 个同学总共最多可以看几场电影呢？
【难度】
【出处】
无
【标注】
【答案】
$8$
【解析】
每人至多出场 $4$ 次，否则需要见至少 $20$ 人次，必然会有人见超过 $2$ 次．于是 $10$ 个同学最多可以看 $8$ 场电影，下面构造 $8$ 场的例子．
如图．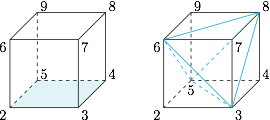
将 $1$ 和 $0$ 取出，剩下的 $8$ 个点看成正方体的 $8$ 个顶点，形成 $6$ 个面：$$\left( {2345} \right),\left( {6789} \right),\left( {2367} \right),\left( {4589} \right),\left( {2569} \right),\left( {3478} \right).$$再取两个正四面体的顶点 $\left( {2479} \right),\left( {3568} \right)$．然后将 $1$ 和 $0$ 放入其中就构造出了 $8$ 场的例子：$$\left( {{\rm{12345}}} \right) , \left( {{\rm{16789}}} \right) , \left( {{\rm{12367}}} \right) , \left( {{\rm{14589}}} \right) , \left( {{\rm{3478}}0} \right) , \left( {{\rm{2569}}0} \right) , \left( {{\rm{2479}}0} \right) , \left( {{\rm{3568}}0} \right).$$
如图．
将 $1$ 和 $0$ 取出，剩下的 $8$ 个点看成正方体的 $8$ 个顶点，形成 $6$ 个面：$$\left( {2345} \right),\left( {6789} \right),\left( {2367} \right),\left( {4589} \right),\left( {2569} \right),\left( {3478} \right).$$再取两个正四面体的顶点 $\left( {2479} \right),\left( {3568} \right)$．然后将 $1$ 和 $0$ 放入其中就构造出了 $8$ 场的例子：$$\left( {{\rm{12345}}} \right) , \left( {{\rm{16789}}} \right) , \left( {{\rm{12367}}} \right) , \left( {{\rm{14589}}} \right) , \left( {{\rm{3478}}0} \right) , \left( {{\rm{2569}}0} \right) , \left( {{\rm{2479}}0} \right) , \left( {{\rm{3568}}0} \right).$$
答案
解析
备注
