有 $n$ 支队伍参加单循环比赛，若某三支队伍 $A,B,C$ 出现 $A$ 击败 $B$，$B$ 击败 $C$，$C$ 击败 $A$，则称三支队伍 $A,B,C$ 构成一个“循环小组”．
【难度】
【出处】
无
【标注】
-
证明：如果没有人全胜，那么必然存在“循环小组”；标注答案略解析假设 $A$ 的获胜场次最多，为 $k$ 场．由于 $A$ 没有全胜，于是在剩下的 $\left( {n - k} \right)$ 个人中一定有 $C$ 胜 $A$．在 $A$ 胜的 $k$ 个人中，如果没有人胜 $C$，那么 $C$ 至少胜了 $\left( {k + 1} \right)$ 场，与假设矛盾，于是存在这样的三个人．
-
请问“循环小组”的最大和最小值分别是多少？标注答案当 $n$ 为奇数时，“循环小组”的最大值为 $\dfrac{1}{{24}}n\left( {n - 1} \right)\left( {n + 1} \right)$，
当 $n$ 为偶数时，“循环小组”的最大值为 $\dfrac{1}{{24}}n\left( {n - 2} \right)\left( {n + 2} \right)$；
“循环小组”的最小值为 $0$解析设 $n$ 支队伍分别赢了 ${a_1} , {a_2} , \cdots , {a_n}$ 场比赛，则$$\displaystyle \sum\limits_{k = 1}^n {{a_k}} = {\rm{C}}_n^2 = \dfrac{{n\left( {n - 1} \right)}}{2}.$$若某三支队伍的内部比赛中，有一支队伍赢了两场，那么它就不是“循环小组”；若某三支队伍不是“循环小组”，那么就一定有且仅有一支队伍赢了两场．因此“循环小组”数为$${\rm{C}}_n^3 - \left( {{\rm{C}}_{{a_1}}^2 + {\rm{C}}_{{a_2}}^2 + \cdots + {\rm{C}}_{{a_n}}^2} \right).$$不难通过调整法证明当 ${a_1} , {a_2} , \cdots , {a_n}$ 尽量平均时（$\left| {{a_i} - {a_j}} \right| \leqslant 1$）“循环小组”数最大．构造是容易的，将 $n$ 支队伍排成一圈，然后间隔为奇数顺时针，间隔为偶数逆时针标记即可，如图．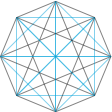
此时可得“循环小组”的最大值为：情形一 $n$ 为奇数时，${a_1} = {a_2} = \cdots = {a_n} = k = \dfrac{{n - 1}}{2}$
于是\[\begin{split}{\rm{C}}_n^3 - n{\rm{C}}_{\frac{{n - 1}}{2}}^2 &= \dfrac{1}{6}n\left( {n - 1} \right)\left( {n - 2} \right) - \dfrac{1}{8}n\left( {n - 1} \right)\left( {n - 3} \right) \\&= \dfrac{1}{{24}}n\left( {n - 1} \right)\left( {n + 1} \right),\end{split}\]情形二 $n$ 为偶数时，${a_1} , {a_2} , \cdots , {a_n}$ 中有 $\dfrac{n}{2}$ 个 $\dfrac{n}{2}$ 和 $\dfrac{n}{2}$ 个 $\dfrac{n}{2} - 1$．
于是\[\begin{split}{\rm{C}}_n^3 - \dfrac{n}{2}{\rm{C}}_{\frac{n}{2}}^2 - \dfrac{n}{2}{\rm{C}}_{\frac{n}{2} - 1}^2& = \dfrac{1}{6}n\left( {n - 1} \right)\left( {n - 2} \right) - \dfrac{1}{{16}}{n^2}\left( {n - 2} \right) - \dfrac{1}{{16}}n\left( {n - 2} \right)\left( {n - 4} \right) \\&= \dfrac{1}{{24}}n\left( {n - 2} \right)\left( {n + 2} \right),\end{split}\]而“循环小组”的最小值为 $0$，只需要将队伍从 $1 , 2 , \cdots , n$ 编号，编号大的赢了编号小的即可．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
