情形一 当 $\triangle PQR$ 的直角顶点在 $\triangle ABC$ 的斜边上时，如图1所示．
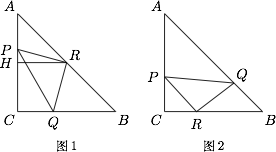
易知 $P,C,Q,R$ 四点共圆，所以$$\angle APR=\angle CQR=180^\circ-\angle BQR,$$故$$\sin\angle APR=\sin\angle BQR.$$在 $\triangle APR,\triangle BQR$ 中分别应用正弦定理得$$\dfrac{PR}{\sin A}=\dfrac{AR}{\sin\angle APR} , \dfrac{QR}{\sin B}=\dfrac{BR}{\sin\angle BQR},$$又因为$$\angle A=\angle B=45^\circ , PR=QR,$$所以 $AR=BR$，即 $R$ 为 $AB$ 中点．
过 $R$ 作 $RH\perp AC$ 于 $H$，则$$PR\geqslant RH=\dfrac12BC,$$所以$$\dfrac{S_{\triangle PQR}}{S_{\triangle ABC}}=\dfrac{PR^2}{BC^2}\geqslant\dfrac14,$$此时 $\dfrac{S_{\triangle PQR}}{S_{\triangle ABC}}$ 的最小值为 $\dfrac14$．
情形二 当 $\triangle PQR$ 的直角顶点在 $\triangle ABC$ 的直角边上时，如图2所示，
设 $BC=1,CR=x,0\leqslant x\leqslant1,\angle BRQ=\alpha,0<\alpha<\dfrac{\pi}{2}$，则$$\angle CPR=90^\circ-\angle PRC=\angle BRQ=\alpha.$$在 $\mathrm{Rt}\triangle CPR$ 中，$$PR=\dfrac{CR}{\sin \alpha}=\dfrac{x}{\sin\alpha}.$$在 $\triangle BRQ$ 中，$$\begin{split}BR=1-x , RQ=PR=\dfrac{x}{\sin\alpha},\\\angle RQB=\pi-\angle QRB-\angle B=\dfrac34\pi-\alpha,\end{split}$$由正弦定理，$\dfrac{RQ}{\sin B}=\dfrac{RB}{\sin\angle RQB}$ 可化为$$\dfrac{x}{\sin\alpha}=\dfrac{1}{\cos\alpha+2\sin\alpha},$$因此$$S_{\triangle PQR}=\dfrac12PR^2=\dfrac12\left(\dfrac{1}{\cos\alpha+2\sin\alpha}\right)^2,$$从而$$\begin{split}\dfrac{S_{\triangle PQR}}{S_{\triangle ABC}}&=\left(\dfrac{1}{\cos\alpha+2\sin\alpha}\right)^2\\&\geqslant\dfrac{1}{(1+2^2)(\cos^2\alpha+\sin^2\alpha)}\\&=\dfrac15,\end{split}$$当且仅当 $\alpha=\arctan2$ 取等号，此时 $\dfrac{S_{\triangle PQR}}{S_{\triangle ABC}}$ 的最小值为 $\dfrac15$．
综上知，$\dfrac{S_{\triangle PQR}}{S_{\triangle ABC}}$ 的最小值为 $\dfrac15$．