已知 $x\in \mathbb{R}$，用 $[x]$ 表示不超过 $x$ 的最大整数，记 $\{x\}=x-[x]$，若 $a\in(0,1)$，则 $\{a\}$ 与 $\left\{a+\dfrac 12\right \}$ 的大小关系是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
A
【解析】
$y=\{x\}$ 是关于 $x$ 的函数，可以通过图象掌握函数 $y=\{x\}$．
先作出 $y=[x]$ 的图象，如下：
于是我们得到函数 $g(x)=\{x\}$ 的图象如下：
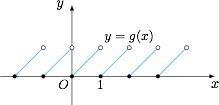题意即比较函数$$g(x)=\{x\}$$和函数$$h(x)=\left\{x+\dfrac 12\right\}$$的图象在 $x\in(0,1)$ 时的位置关系．如图，$y=h(x)$ 的图象可以由 $y=g(x)$ 的图象向左平移 $\dfrac 12$ 个单位得到：
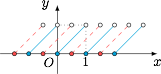可以发现当 $0<x<\dfrac{1}{2}$ 时，有$$\left\{x+\dfrac{1}{2}\right\}>\{x\};$$当 $\dfrac{1}{2}\leqslant x < 1$ 时，有$$\left\{x+\dfrac{1}{2}\right\}<\left\{x\right\}.$$
先作出 $y=[x]$ 的图象，如下：
于是我们得到函数 $g(x)=\{x\}$ 的图象如下：题意即比较函数$$g(x)=\{x\}$$和函数$$h(x)=\left\{x+\dfrac 12\right\}$$的图象在 $x\in(0,1)$ 时的位置关系．如图，$y=h(x)$ 的图象可以由 $y=g(x)$ 的图象向左平移 $\dfrac 12$ 个单位得到：可以发现当 $0<x<\dfrac{1}{2}$ 时，有$$\left\{x+\dfrac{1}{2}\right\}>\{x\};$$当 $\dfrac{1}{2}\leqslant x < 1$ 时，有$$\left\{x+\dfrac{1}{2}\right\}<\left\{x\right\}.$$
题目
答案
解析
备注
