已知直线 $ax+by=4$ 与不等式组 $\begin{cases} 2x-5y+8\geqslant 0,\\ 2x+y-4\leqslant 0,\\ x+2y+4 \geqslant 0,\end{cases}$ 表示的平面区域无公共点，则 $a+b$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
【解析】
如图，直线 $y=x$ 被题中不等式组所表示的平面区域截得的部分为 $\left[-\dfrac 43,\dfrac 43\right]$．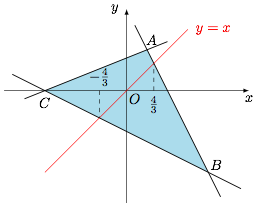
根据题意有\[\forall t\in\left[-\dfrac 43,\dfrac 43\right],t(a+b)\ne 4,\]于是 $a+b\in (-3,3)$．另一方面，当直线 $ax+by=4$ 分别取直线 $AB$ 和 $BC$ 时，$a+b$ 分别趋于 $3$ 和 $-3$．
综上所述，$a+b$ 的取值范围是 $(-3,3)$．
根据题意有\[\forall t\in\left[-\dfrac 43,\dfrac 43\right],t(a+b)\ne 4,\]于是 $a+b\in (-3,3)$．另一方面，当直线 $ax+by=4$ 分别取直线 $AB$ 和 $BC$ 时，$a+b$ 分别趋于 $3$ 和 $-3$．综上所述，$a+b$ 的取值范围是 $(-3,3)$．
题目
答案
解析
备注
