已知 $f(x)=\dfrac {3x+1}{2x-1}$，画出函数 $f(x)$ 的草图，并写出 $f(x)$ 的定义域，值域以及单调性．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图．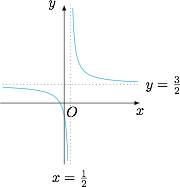
函数 $f(x)$ 的定义域为 $\left(-\infty,\dfrac 12\right)\cup\left(\dfrac 12,+\infty\right)$，值域为 $\left(-\infty,\dfrac 32\right)\cup\left(\dfrac 32,+\infty\right)$，函数 $f(x)$ 在区间 $\left(-\infty,\dfrac 12\right)$ 和 $\left(\dfrac 12,+\infty\right)$ 均单调递减．
函数 $f(x)$ 的定义域为 $\left(-\infty,\dfrac 12\right)\cup\left(\dfrac 12,+\infty\right)$，值域为 $\left(-\infty,\dfrac 32\right)\cup\left(\dfrac 32,+\infty\right)$，函数 $f(x)$ 在区间 $\left(-\infty,\dfrac 12\right)$ 和 $\left(\dfrac 12,+\infty\right)$ 均单调递减．
答案
解析
备注
