画出下列函数的草图，并写出单调区间．
$(1)$ $f(x)=\dfrac {x}{x^2+1}$，$g(x)=\dfrac {x}{x^2-1}$；
$(2)$ $f(x)=\dfrac {1}{x^2-2x+3}$，$g(x)=\dfrac {1}{x^2-2x+1}$，$h(x)=\dfrac {1}{x^2-2x}$；
$(3$）$f(x)=\dfrac {x-1}{x^2+x}$，$g(x)=\dfrac {x^2-x+1}{x^2+x+1}$．
$(1)$ $f(x)=\dfrac {x}{x^2+1}$，$g(x)=\dfrac {x}{x^2-1}$；
$(2)$ $f(x)=\dfrac {1}{x^2-2x+3}$，$g(x)=\dfrac {1}{x^2-2x+1}$，$h(x)=\dfrac {1}{x^2-2x}$；
$(3$）$f(x)=\dfrac {x-1}{x^2+x}$，$g(x)=\dfrac {x^2-x+1}{x^2+x+1}$．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
$(1)$ 函数 $f(x)$ 是基本对勾函数 $y=x+\dfrac 1x$ 的补充倒数函数，函数 $g(x)$ 是基本对勾函数 $y=x-\dfrac 1x$ 的补充倒数函数，如图．
函数 $f(x)$ 的单调递增区间是 $(-1,1)$，单调递减区间是 $(-\infty,-1)$ 和 $(1,+\infty)$；函数 $g(x)$ 没有单调递增区间，单调递减区间是 $(-\infty,-1)$，$(-1,1)$，$(1,+\infty)$．
$(2)$ 函数 $f(x)$ 是二次函数 $y=x^2-2x+3$ 的倒数函数；函数 $g(x)$ 是二次函数 $y=x^2-2x+1$ 的补充倒数函数；函数 $h(x)$ 是二次函数 $y=x^2-2x$ 的补充倒数函数，如图．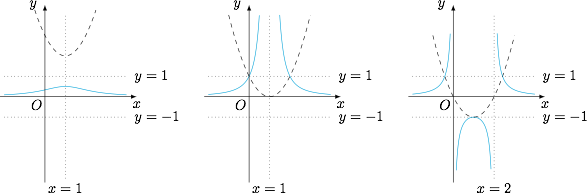
$(3)$ 考虑到 $f(x)$ 是对勾函数 $y=x+2+\dfrac{2}{x-1}$ 的补充倒数函数，因此图象如左图．
又$$g(x)=1+\dfrac{-2x}{x^2+x+1},$$而函数 $y=\dfrac{-2x}{x^2+x+1}$ 是对勾函数 $y=-\dfrac 12x-\dfrac 12-\dfrac 1{2x}$ 的倒数函数，如右图．
函数 $f(x)$ 的单调递增区间是 $(-1,1)$，单调递减区间是 $(-\infty,-1)$ 和 $(1,+\infty)$；函数 $g(x)$ 没有单调递增区间，单调递减区间是 $(-\infty,-1)$，$(-1,1)$，$(1,+\infty)$．$(2)$ 函数 $f(x)$ 是二次函数 $y=x^2-2x+3$ 的倒数函数；函数 $g(x)$ 是二次函数 $y=x^2-2x+1$ 的补充倒数函数；函数 $h(x)$ 是二次函数 $y=x^2-2x$ 的补充倒数函数，如图．
$(3)$ 考虑到 $f(x)$ 是对勾函数 $y=x+2+\dfrac{2}{x-1}$ 的补充倒数函数，因此图象如左图．又$$g(x)=1+\dfrac{-2x}{x^2+x+1},$$而函数 $y=\dfrac{-2x}{x^2+x+1}$ 是对勾函数 $y=-\dfrac 12x-\dfrac 12-\dfrac 1{2x}$ 的倒数函数，如右图．
答案
解析
备注
