已知二次函数 $f\left( x \right) = {x^2} + px + q$，其中 $p,q\in\mathbb R$．方程 $f\left( {f\left( x \right)} \right) = 0$ 有且只有一解，求证：$p \geqslant 0$，$q \geqslant 0$．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设 $f(x)$ 的两根为 $x_1,x_2$ 且 $x_1\leqslant x_2$，则函数 $y=f(x)$ 的图象与两条平行直线 $y=x_1,y=x_2$ 有且只有一个公共点，如图．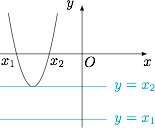
因此函数 $y=f(x)$ 的最小值为 $x_2$，且 $x_2\leqslant 0$，因此 $x_1\leqslant x_2\leqslant 0$，由韦达定理即得．
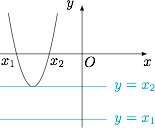因此函数 $y=f(x)$ 的最小值为 $x_2$，且 $x_2\leqslant 0$，因此 $x_1\leqslant x_2\leqslant 0$，由韦达定理即得．
答案
解析
备注
