如图,在 $\triangle{ABC}$ 中,$DE\parallel BC$,$\triangle{ADE}$ 的内切圆与 $DE$ 切于点 $M$,$\triangle{ABC}$ 的 $BC$ 边上的旁切圆切 $BC$ 于点 $N$,点 $P$ 是 $BE$ 与 $CD$ 的交点,求证:$M,N,P$ 三点共线.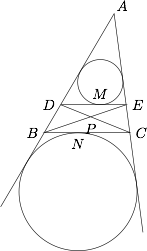

【难度】
【出处】
2009年全国高中数学联赛江苏省复赛(二试)
【标注】
【答案】
略
【解析】
设 $BE$ 与 $MN$ 交于点 $P'$,因为 $DE\parallel BC$,所以$$\dfrac{BP}{PE}=\dfrac{BC}{DE},\dfrac{BP'}{P'E}=\dfrac{BN}{EM}.$$故只需证明 $\dfrac{BC}{DE}=\dfrac{BN}{EM}$ 或 $\dfrac{BN}{BC}=\dfrac{EM}{DE}$.
如图,设 $O_1,O_2$ 分别为三角形的内切圆与旁切圆的圆心,$F,G,H,I$ 为切点,则\[\begin{split}EM&=\dfrac 12(AE+DE-AD),\\ AH&=AB+BH=AB+BN,\\ AH&=AI=\dfrac 12(AB+BC+AC),\\ BN&=AH-AB=\dfrac 12(AC+BC-AB).\end{split}\]又因为 $\triangle{ADE}\backsim \triangle{ABC}$,故可设$$\dfrac{AB}{AD}=\dfrac{BC}{DE}=\dfrac{AC}{AE}=k,$$则\[\begin{split}\dfrac{BN}{BC}&=\dfrac{\dfrac 12(AC+BC-AB)}{BC}\\&=\dfrac{k\cdot AE+k\cdot DE-k\cdot AD}{2k\cdot DE}\\&=\dfrac{AE+DE-AD}{2DE}\\&=\dfrac{EM}{DE},\end{split}\]故结论成立.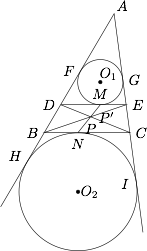
如图,设 $O_1,O_2$ 分别为三角形的内切圆与旁切圆的圆心,$F,G,H,I$ 为切点,则\[\begin{split}EM&=\dfrac 12(AE+DE-AD),\\ AH&=AB+BH=AB+BN,\\ AH&=AI=\dfrac 12(AB+BC+AC),\\ BN&=AH-AB=\dfrac 12(AC+BC-AB).\end{split}\]又因为 $\triangle{ADE}\backsim \triangle{ABC}$,故可设$$\dfrac{AB}{AD}=\dfrac{BC}{DE}=\dfrac{AC}{AE}=k,$$则\[\begin{split}\dfrac{BN}{BC}&=\dfrac{\dfrac 12(AC+BC-AB)}{BC}\\&=\dfrac{k\cdot AE+k\cdot DE-k\cdot AD}{2k\cdot DE}\\&=\dfrac{AE+DE-AD}{2DE}\\&=\dfrac{EM}{DE},\end{split}\]故结论成立.

答案
解析
备注