已知函数\[f(x)=\begin{cases}\log_ax,&x>0,\\|x+3|,&-4 \leqslant x<0,\end{cases}\]其中 $a>0$ 且 $a\ne 1$．若函数 $f(x)$ 的图象上有且只有一对点关于 $y$ 轴对称，则 $a$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
无
【标注】
【答案】
D
【解析】
原问题等价于将 $f(x)$ 在 $y$ 轴左侧的图象关于 $y$ 轴反射，与 $f(x)$ 在 $y$ 轴右侧的图象有且只有一个交点．如图：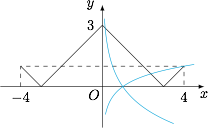
当 $0<a<1$ 时一定满足；当 $a>1$ 时，需要有 ${\log_a}4>1$，解得 $a<4$．
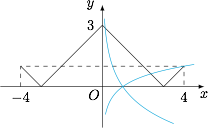当 $0<a<1$ 时一定满足；当 $a>1$ 时，需要有 ${\log_a}4>1$，解得 $a<4$．
题目
答案
解析
备注
