已知椭圆 $E:\dfrac{x^2}{9}+\dfrac{y^2}{5}=1$ 的左焦点为 $F_1$，过 $F_1$ 的直线 $l$ 交椭圆 $E$ 于 $A,B$ 两点，点 $Q$ 的坐标为 $\left(-\dfrac92,0\right)$．若 $\overrightarrow{QB}\perp\overrightarrow{AB}$，求直线 $l$ 的斜率．
【难度】
【出处】
2015年全国高中数学联赛新疆预赛
【标注】
【答案】
$\sqrt3$
【解析】
设直线 $AB$ 的倾斜角为 $\angle AF_1F_2=\theta$，椭圆的右焦点为 $F_2$，如图．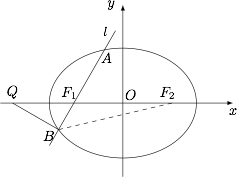
容易知道 $\angle BF_1F_2=\pi-\theta$．
在 $\triangle BF_1F_2$ 中，设 $|BF_1|=x$，则$$|BF_2|=2a-x=6-x.$$由余弦定理可知$$|BF_2|^2=|BF_1|^2+|F_1F_2|^2-2|BF_1|\cdot|F_1F_2|\cdot\cos(\pi-\theta),$$整理得$$(6-x)^2=x^2+4^2+8x\cos\theta,$$解得$$x=|BF_1|=\dfrac{5}{3+2\cos\theta}.$$在 $\mathrm{Rt}\triangle QBF_1$ 中，$$|BF_1|=|QF_1|\cos\theta=\dfrac52\cos\theta,$$所以$$\dfrac{5}{3+2\cos\theta}=\dfrac52\cos\theta,$$整理得$$(2\cos\theta-1)(\cos\theta+2)=0,$$因此 $\cos\theta=\dfrac12$，结合 $0<\theta<\pi$，所以 $\theta=\dfrac{\pi}{3}$，从而直线的斜率为 $\sqrt3$．
容易知道 $\angle BF_1F_2=\pi-\theta$．在 $\triangle BF_1F_2$ 中，设 $|BF_1|=x$，则$$|BF_2|=2a-x=6-x.$$由余弦定理可知$$|BF_2|^2=|BF_1|^2+|F_1F_2|^2-2|BF_1|\cdot|F_1F_2|\cdot\cos(\pi-\theta),$$整理得$$(6-x)^2=x^2+4^2+8x\cos\theta,$$解得$$x=|BF_1|=\dfrac{5}{3+2\cos\theta}.$$在 $\mathrm{Rt}\triangle QBF_1$ 中，$$|BF_1|=|QF_1|\cos\theta=\dfrac52\cos\theta,$$所以$$\dfrac{5}{3+2\cos\theta}=\dfrac52\cos\theta,$$整理得$$(2\cos\theta-1)(\cos\theta+2)=0,$$因此 $\cos\theta=\dfrac12$，结合 $0<\theta<\pi$，所以 $\theta=\dfrac{\pi}{3}$，从而直线的斜率为 $\sqrt3$．
答案
解析
备注
