2015年全国高中数学联赛新疆预赛

略

用 $u_1,u_2,\cdots,u_9$，代表参加聚会的九个同学，构造一个 $G=(V,E)$ 如下：$$V=\{ u_1,u_2,\cdots,u_9\},$$其中 $u_i$ 和 $u_j$ 连一条边（记作 $u_iu_j\in E$）当且仅当 $u_i$ 和 $u_j$ 喝过酒．
我们用 $N(u_i)$ 表示 $u_i$ 的邻点集（即和 $u_i$ 喝过酒的人），而 $d(u_i)=|N(u_i)|$ 表示 $u_i$ 的度数（即和 $u_i$ 喝过酒的人数）．这样，“任何两个人 $u_i,u_j$ 恰好只和某个人 $u_k$ 喝过酒”可表示为$$N(u_i)\cap N(u_j)=\{u_k\}.$$按图的构造，我们只需证明 $G$ 中恰有一个顶点的度数为 $8$，其余顶点的度数为 $2$．
不失一般性，设 $N(u_9)=\{u_1,u_2,\cdots,u_k\}$，这里 $k\leqslant8$．
依假设有 $u\in N(u_9)$ 使得$$N(u_1)\cap N(u_9)=\{u\},$$不妨设 $u=u_2$，类似的对于 $u_3\in N(u_9)-\{u_1,u_2\}$，有 $v\in N(u_9)-\{u_1,u_2,u_3\}$ 使得$$N(u_3)\cap N(u_9)=\{v\},$$故不妨设 $v=u_4$，依此类推，我们得到 $N(u_9)$ 中的点两两配对，每一对恰有一条边相连．
不妨设$$u_1u_2,u_3u_4,\cdots,u_{k-1}u_k\in E,$$显然，$k$ 必然是偶数，如图 $(a)$ 所示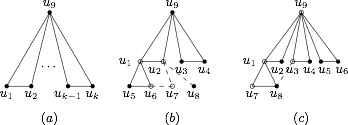．由于 $u_9$ 可以是任意一个点，事实上，我们证明了 $G$ 的任一点 $u$ 的邻集，$N(u)$ 恰含偶数个点，他们两两配对，每一对都有一条边相连，如果 $k=8$，则问题已解决．否则 $G$ 有两个相邻的点，不妨设 $u_1,u_9$ 使得 $d(u_1)$ 和 $d_{u_9}$ 都是偶数，并且不小于 $4$，以下我们分两种情况：
情形一 $d(u_1)=4=d(u_9)$．
可设\[\begin{split}&N(u_1)=\{u_9,u_2,u_5,u_6\},\\&N(u_9)=\{u_1,u_2,u_3,u_4\},\end{split}\]如图 $(b)$ 所示，此时，我们考虑另外两个点 $u_7$ 和 $u_8$．
设 $N(u_7)\cap N(u_8)=\{v\}$，那么$$v\in\{u_2,u_3,u_4,u_5,u_6\}.$$如果 $v=u_2$，则 $u_7u_6\in E$．
但是这样一来，$u_1u_2u_7u_6$ 构成一个 $4$ 圈，此时$$N(u_1)\cap N(u_7)\supseteq\{u_2,u_6\},$$矛盾．当 $v=u_3,u_4,u_5u_6$ 时，同样可以导出 $G$ 中的 $4$ 圈．
情形二 $d(u_1)=4,d(u_9)=6$．
不妨设\[\begin{split}&N(u_9)=\{u_1,u_2,u_3,u_4,u_5,u_6\},\\&N(u_1)=\{u_2,u_9,u_7,u_8\},\end{split}\]如图 $(c)$ 所示，此时考虑到$$|N(u_7)\cap N(u_3)|=1,$$必然有 $u_8u_3\in E$，从而 $u_8u_3u_9u_1$ 构成一个 $4$ 圈，矛盾．