已知平行四边形 $ABCD$ 满足 $\angle{BAD}=90^{\circ}$,向四边形外部作 $\triangle{DCE}$ 和 $\triangle{BCF}$ 使得 $\angle{EDC}=\angle{CBF}$,$\angle{DCE}=\angle{BFC}$,连结 $EF$,向 $\triangle{CEF}$ 外部作 $\triangle{EFG}$ 使得 $\angle{FEG}=\angle{CED}$.证明:$\triangle{AEF}\cong \triangle{GEF}$.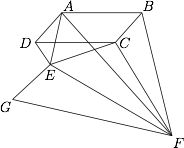

【难度】
【出处】
2009年全国高中数学联赛安徽省预赛
【标注】
【答案】
略
【解析】
由题意知$$\triangle{EDC}\backsim \triangle{CBF}\backsim \triangle{EGF},$$所以$$\dfrac{AB}{DE}=\dfrac{DC}{DE}=\dfrac{BF}{BC}=\dfrac{BF}{AD}.$$又因为 $\angle{EDA}=\angle{ABF}$,所以 $\triangle{EDA}\backsim \triangle{ABF} $,故$$\dfrac{AF}{AE}=\dfrac{AB}{DE}=\dfrac{DC}{DE}=\dfrac{GF}{GE}.$$由于\[\begin{split}\angle{EAF}&=\pi-\angle{DAE}-\angle{FAB}-\angle{ABC}\\&=\pi-\angle{AFB}-\angle{FAB}-\angle{ABC}\\&=\angle{CBF}\\&=\angle{EGF},\end{split}\]因此 $\triangle{AEF}\cong \triangle{GEF}$.
答案
解析
备注