如图，$\triangle ABC$ 内接于圆 $O$，$P$ 为 $\overparen{BC}$ 上一点，点 $K$ 在线段 $AP$ 上，使得 $BK$ 平分 $\angle ABC$．过 $K,P,C$ 三点的圆 $\Omega$ 与边 $AC$ 交于点 $D$，连接 $BD$ 交圆 $\Omega$ 于点 $E$，连接 $PE$ 并延长与边 $AB$ 交于点 $F$．证明：$\angle ABC=2\angle FCB$．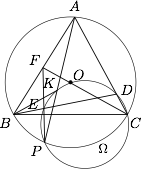
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
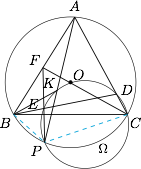注意此时 $C,D,L,K,E,P$ 六点均在圆 $\Omega$ 上，结合 $A,B,P,C$ 四点共圆，可知$$\angle FEB=\angle DEP=180^\circ-\angle DCP=\angle ABP=\angle FBP.$$因此 $\triangle FBE\backsim\triangle FPB$，故 $FB^2=FE\cdot FP$．结合圆幂定理知$$FE\cdot FP=Fl\cdot FC=FB^2,$$从而 $\triangle FBL\backsim \triangle FCB$．因此$$\angle FLB=\angle FBC=\angle APC=\angle KPC=\angle FLK,$$即 $B,K,L$ 三点共线．再根据 $\triangle FBL\backsim \triangle FCB$，得$$\angle FCB=\angle FBL=\angle FBE=\dfrac12\angle ABC,$$即 $\angle ABC=2\angle FCB$．
对圆内接广义六边形 $DCPEKL$ 应用帕斯卡定理可知，$DC$ 与 $KP$ 的交点 $A$，$CL$ 与 $PE$ 的交点 $F$，$LK$ 与 $ED$ 的交点 $B'$ 共线，因此 $B'=B$，所以 $B,K,L$ 共线．根据 $A,B,P,C$ 四点共圆及 $L,K,P,C$ 四点共圆，得$$\angle ABC=\angle APC=\angle FLK=\angle FCB+\angle LBC,$$又由 $BK$ 平分 $\angle ABC$ 知，$\angle LBC=\dfrac12\angle ABC$，从而 $\angle ABC=2\angle FBC$．
答案
解析
备注
