已知点 $A(-1,0)$，$B(1,0)$，$C(0,1)$，直线 $y=ax+b$（$a>0$）将 $\triangle ABC$ 分割为面积相等的两部分，则 $b$ 的取值范围是 \((\qquad)\)
【难度】
【出处】
2013年高考新课标Ⅱ卷（理）
【标注】
【答案】
B
【解析】
按直线 $y=ax+b$ 是否与斜边 $AB$ 相交分类讨论，讨论的分界点为直线过点 $A$，也即 $a=\dfrac 13$．
情形一 直线 $l$ 与边 $AC$ 和 $BC$ 分别交于 $D,E$，交 $y$ 轴于 $F$ 点，如图．此时 $a$ 的取值范围是 $\left(0,\dfrac 13\right)$．
设 $D(x_1,y_1)$，$E(x_2,y_2)$，则将直线 $y=ax+b$ 与相交直线\[AC\cup BC:(y-1)^2-x^2=0\]联立，可得\[(a^2-1)x^2+2a(b-1)x+(b-1)^2=0,\]于是\[\begin{split} \triangle CDE&=\dfrac 12 \cdot CD\cdot CE\\
&=\dfrac 12\cdot \sqrt 2|x_1|\cdot \sqrt 2|x_2|\\
&=|x_1x_2|\\
&=\dfrac{(1-b)^2}{1-a^2},\end{split}\]从而\[(1-b)^2=\dfrac 12(1-a^2),\]因此 $b$ 的取值范围是 $\left(1-\dfrac{\sqrt 2}2,\dfrac 13\right)$．
情形二 直线 $l$ 与边 $AB$ 和 $BC$ 分别交于 $D,E$，交 $y$ 轴于 $F$ 点，如图．此时 $a$ 的取值范围是 $\left[\dfrac 13,+\infty\right)$．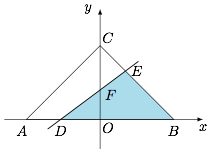
设 $D(x_1,y_1)$，$E(x_2,y_2)$，则\[x_1=-\dfrac ba,x_2=\dfrac{1-b}{a+1},\]于是\[\begin{split}\triangle BDE&=\dfrac {\sqrt 2}4\cdot BE\cdot BD\\
&=\dfrac{\sqrt 2}4\cdot \sqrt 2(1-x_2)\cdot (1-x_1)\\
&=\dfrac 12\cdot \dfrac{a+b}{a+1}\cdot \dfrac{a+b}{a}\\
&=\dfrac{(a+b)^2}{2a(a+1)},\end{split}\]从而\[(a+b)^2=a(a+1),\]即\[a=\dfrac{b^2}{1-2b},\]因此 $b$ 的取值范围是 $\left[\dfrac 13,\dfrac 12\right)$．
综上所述，$b$ 的取值范围是 $\left(1-\dfrac{\sqrt 2}2,\dfrac 12\right)$．
设 $D(x_1,y_1)$，$E(x_2,y_2)$，则将直线 $y=ax+b$ 与相交直线\[AC\cup BC:(y-1)^2-x^2=0\]联立，可得\[(a^2-1)x^2+2a(b-1)x+(b-1)^2=0,\]于是\[\begin{split} \triangle CDE&=\dfrac 12 \cdot CD\cdot CE\\&=\dfrac 12\cdot \sqrt 2|x_1|\cdot \sqrt 2|x_2|\\
&=|x_1x_2|\\
&=\dfrac{(1-b)^2}{1-a^2},\end{split}\]从而\[(1-b)^2=\dfrac 12(1-a^2),\]因此 $b$ 的取值范围是 $\left(1-\dfrac{\sqrt 2}2,\dfrac 13\right)$．
设 $D(x_1,y_1)$，$E(x_2,y_2)$，则\[x_1=-\dfrac ba,x_2=\dfrac{1-b}{a+1},\]于是\[\begin{split}\triangle BDE&=\dfrac {\sqrt 2}4\cdot BE\cdot BD\\&=\dfrac{\sqrt 2}4\cdot \sqrt 2(1-x_2)\cdot (1-x_1)\\
&=\dfrac 12\cdot \dfrac{a+b}{a+1}\cdot \dfrac{a+b}{a}\\
&=\dfrac{(a+b)^2}{2a(a+1)},\end{split}\]从而\[(a+b)^2=a(a+1),\]即\[a=\dfrac{b^2}{1-2b},\]因此 $b$ 的取值范围是 $\left[\dfrac 13,\dfrac 12\right)$．
综上所述，$b$ 的取值范围是 $\left(1-\dfrac{\sqrt 2}2,\dfrac 12\right)$．
题目
答案
解析
备注
