在平面直角坐标系 $xOy$ 中，二次函数 $y=mx^2-(2m+1)x+m-5$ 的图象与 $x$ 轴有两个公共点，
【难度】
【出处】
无
【标注】
-
若 $m$ 取满足条件的最小整数，当 $n\leqslant x \leqslant 1$ 时，函数值 $y$ 的取值范围是 $-6\leqslant y \leqslant 4-n$，求 $n$ 的值；标注答案$n$ 的值为 $-2$解析根据已知可得 $\Delta=[-(2m+1)]^2-4m(m-5)>0$，
所以 $m>-\dfrac {1}{24}$，
又因为 $m\ne 0$，所以 $m=1$，
图象的对称轴为直线 $x=\dfrac 32$．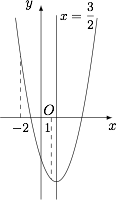
当 $n\leqslant x \leqslant 1<\dfrac 32$ 时，
函数值 $y$ 随自变量 $x$ 的增大而减小，
因为函数值 $y$ 的取值范围是 $-6\leqslant y \leqslant 4-n$，
所以当 $x=1$ 时，函数值为 $-6$，当 $x=n$ 时，函数值为 $4-n$，
所以 $n^2-3n-4=4-n$，解得 $n=-2$ 或 $n=4$（不合题意，舍去），
所以 $n$ 的值为 $-2$． -
将此二次函数平移，使平移后的图象经过原点 $O$，设平移后的图象对应的函数表达式为 $y=a(x-h)^2+k$，当 $x<2$ 时，$y$ 随 $x$ 的增大而减小，求 $k$ 的取值范围．标注答案$k$ 的取值范围是 $k\leqslant -4$解析因为 $a=1$，函数图象经过原点，
所以 $y=x^2-2hx+h^2+k$，$h^2+k=0$，
所以 $k=-h^2$，
因为当 $x<2$ 时，$y$ 随 $x$ 的增大而减小，
所以 $h\geqslant 2$，
所以 $k\leqslant -4$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
