在平面直角坐标系 $xOy$ 中，抛物线 $C_1:y=x^2-6x+5$ 与 $x$ 轴交于点 $A,B$（点 $A$ 在点 $B$ 的左侧），将抛物线 $C_1$ 平移，得到抛物线 $C_2$ 的顶点为 $(0,-1)$，抛物线 $C_1$ 的对称轴于两条抛物线 $C_1,C_2$ 围成的密闭图形为 $M$，直线 $l:y=kx+m$（$k\ne 0$）经过点 $B$，若直线 $l$ 与图形 $M$ 有公共点，求 $k$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$k$ 的取值范围是 $-4\leqslant k \leqslant 2$ 且 $k\ne 0$
【解析】
因为 $C_1:y=(x-3)^2-4$，所以顶点 $D(3,-4)$．
平移后得到的新抛物线 $C_2$ 的顶点为 $(0,-1)$，
所以抛物线 $C_2$ 的表达式为 $y=x^2-1$，
所以抛物线 $C_1$ 的对称轴 $x=3$ 与抛物线 $C_2$ 的交点为 $E(3,8)$．
① 当直线 $l$ 过点 $B(5,0)$ 和点 $D(3,-4)$ 时，
得 $\begin{cases}5k+m=0,\\ 3k+m=-4,\end{cases}$ 解得 $\begin{cases}k=2,\\m=-10.\end{cases}$
此时直线 $l$ 为 $y=2x-10$；
② 当直线 $l$ 过点 $B(5,0)$ 和点 $E(3,8)$ 时，
得 $\begin{cases}5k+m=0,\\ 3k+m=8,\end{cases}$ 解得 $\begin{cases}k=-4,\\m=20.\end{cases}$此时直线 $l$ 为 $y=-4x+20$．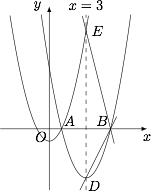
结合函数图象，得满足题意的 $k$ 的取值范围是 $-4\leqslant k \leqslant 2$ 且 $k\ne 0$．
平移后得到的新抛物线 $C_2$ 的顶点为 $(0,-1)$，
所以抛物线 $C_2$ 的表达式为 $y=x^2-1$，
所以抛物线 $C_1$ 的对称轴 $x=3$ 与抛物线 $C_2$ 的交点为 $E(3,8)$．
① 当直线 $l$ 过点 $B(5,0)$ 和点 $D(3,-4)$ 时，
得 $\begin{cases}5k+m=0,\\ 3k+m=-4,\end{cases}$ 解得 $\begin{cases}k=2,\\m=-10.\end{cases}$
此时直线 $l$ 为 $y=2x-10$；
② 当直线 $l$ 过点 $B(5,0)$ 和点 $E(3,8)$ 时，
得 $\begin{cases}5k+m=0,\\ 3k+m=8,\end{cases}$ 解得 $\begin{cases}k=-4,\\m=20.\end{cases}$此时直线 $l$ 为 $y=-4x+20$．
结合函数图象，得满足题意的 $k$ 的取值范围是 $-4\leqslant k \leqslant 2$ 且 $k\ne 0$．
答案
解析
备注
