在平面直角坐标系 $xOy$ 中，抛物线 $y=-x^2+2mx-m^2-m+1$，若两点 $A(-1,0),B(1,0)$，且该抛物线与线段 $AB$ 始终有交点，请写出 $m$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$m$ 的取值范围为 $-3\leqslant m\leqslant 1$
【解析】
因为 $y=-(x-m)^2-m+1$，
所以抛物线顶点坐标为 $(m,-m+1)$，
即抛物线的顶点在直线 $y=-x+1$ 上．
当 $y=-x^2+2mx-m^2-m+1$ 过点 $A(-1,0)$ 时，得 $m=-3$ 或 $m=0$（舍）；
当 $y=-x^2+2mx-m^2-m+1$ 过点 $B(1,0)$ 时，得 $m=1$ 或 $m=0$（舍）．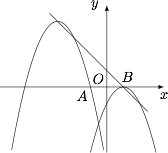
结合函数图像，得 $m$ 的取值范围为 $-3\leqslant m\leqslant 1$．
所以抛物线顶点坐标为 $(m,-m+1)$，
即抛物线的顶点在直线 $y=-x+1$ 上．
当 $y=-x^2+2mx-m^2-m+1$ 过点 $A(-1,0)$ 时，得 $m=-3$ 或 $m=0$（舍）；
当 $y=-x^2+2mx-m^2-m+1$ 过点 $B(1,0)$ 时，得 $m=1$ 或 $m=0$（舍）．
结合函数图像，得 $m$ 的取值范围为 $-3\leqslant m\leqslant 1$．
答案
解析
备注
