在直角坐标系 $xOy$ 中,曲线 $y=x^2+mx-2 $ 与 $x$ 轴交于 $A$,$B$ 两点,点 $ C $ 的坐标为 $(0,1)$,当 $m$ 变化时,解答下列问题:
【难度】
【出处】
2017年高考全国丙卷(文)
【标注】
-
能否出现 $BC\perp AC$ 的情况?说明理由;标注答案不可能出现,理由略解析考虑到 $A,B,D$ 是曲线 $x^2+mx-2-y=0$ 和曲线 $y(y+2)=0$ 的公共点,因此 $\triangle ABD$ 外接圆 $K$ 的方程为\[x^2+mx-2-y+y(y+2)=0,\]即\[x^2+y^2+mx+y-2=0,\]该圆恒过点 $C(0,1)$,因此若 $BC\perp AC$,则 $AB$ 为圆 $K$ 的直径,此时圆 $K$ 关于 $x$ 轴对称,但它与 $y$ 轴的公共点为 $D(0,-2)$ 和 $C(0,1)$ 不对称,矛盾.这就意味着不可能出现 $BC\perp AC$ 的情况.
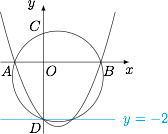
-
证明过 $A$,$B$,$C$ 三点的圆在 $y$ 轴上截得的弦长为定值.标注答案略解析由第 $(1)$ 小题结论,可得 $\triangle ABC$ 的外接圆与 $y$ 轴的公共点为 $D(0,-2)$ 和 $C(0,1)$,因此被 $y$ 轴截得的弦长为定值 $3$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2