在平面直角坐标系中,我们不妨将横坐标、纵坐标均为整数的点称之为"中国结".若二次函数 $y=(k^2-3k+2)x^2+(2k^2-4k+1)x+k^2-k$($k$ 为常数)的图象与 $x$ 轴相交得到两个不同的"中国结",试问该函数的图象与 $x$ 轴所围成的平面图形中(含边界),一共包含有多少个"中国结"?
【难度】
【出处】
无
【标注】
【答案】
该函数的图象与 $x$ 轴所围成的平面图形中(含边界),一共包含 $6$ 个"中国结",分别为:$(-3,0)$,$(-2,0)$,$(-1,0)$,$(-1,1)$,$(0,0)$,$(1,0)$
【解析】
令 $y=0$,即 $(k^2-3k+2)x^2+(2k^2-4k+1)x+k^2-k=0$,
因式分解,得 $[(k-1)x+k][(k-2)x+k-1]=0$.
解得 $x_1=-\dfrac{k}{k-1}=-1-\dfrac 1{k-1}$,$x_2=-\dfrac{k-1}{k-2}=-1-\dfrac 1{k-2}$.
由题意可得 $x_1,x_2$ 均为整数,所以 $\dfrac 1{k-1},\dfrac 1{k-2}$ 也为整数.
设 $\dfrac 1{k-1}=m$($m\ne 0$,$m$ 为整数),则 $k=\dfrac 1m+1$,
所以 $\dfrac 1{k-2}=\dfrac 1{\dfrac 1m+1-2}=\dfrac {m}{1-m}=\dfrac {-(1-m)+1}{1-m}=-1+\dfrac 1{1-m}$,
所以 $1-m=\pm 1$,即 $m_1= 0$(舍去),$m_2=2$,
从而得到 $k=\dfrac 32$.
所以二次函数解析式为 $y=-\dfrac 14x^2-\dfrac 12x+\dfrac 34=-\dfrac 14(x+1)^2+1$.
二次函数图象如图所示,则该函数的图象与 $x$ 轴所围成的平面图形中(含边界),一共包含 $6$ 个"中国结",分别为:$(-3,0)$,$(-2,0)$,$(-1,0)$,$(-1,1)$,$(0,0)$,$(1,0)$.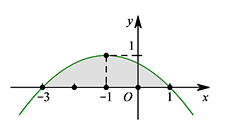
因式分解,得 $[(k-1)x+k][(k-2)x+k-1]=0$.
解得 $x_1=-\dfrac{k}{k-1}=-1-\dfrac 1{k-1}$,$x_2=-\dfrac{k-1}{k-2}=-1-\dfrac 1{k-2}$.
由题意可得 $x_1,x_2$ 均为整数,所以 $\dfrac 1{k-1},\dfrac 1{k-2}$ 也为整数.
设 $\dfrac 1{k-1}=m$($m\ne 0$,$m$ 为整数),则 $k=\dfrac 1m+1$,
所以 $\dfrac 1{k-2}=\dfrac 1{\dfrac 1m+1-2}=\dfrac {m}{1-m}=\dfrac {-(1-m)+1}{1-m}=-1+\dfrac 1{1-m}$,
所以 $1-m=\pm 1$,即 $m_1= 0$(舍去),$m_2=2$,
从而得到 $k=\dfrac 32$.
所以二次函数解析式为 $y=-\dfrac 14x^2-\dfrac 12x+\dfrac 34=-\dfrac 14(x+1)^2+1$.
二次函数图象如图所示,则该函数的图象与 $x$ 轴所围成的平面图形中(含边界),一共包含 $6$ 个"中国结",分别为:$(-3,0)$,$(-2,0)$,$(-1,0)$,$(-1,1)$,$(0,0)$,$(1,0)$.

答案
解析
备注