已知关于 $x$ 的一元二次方程 $x^2+(k-5)x+1-k=0$，其中 $k$ 为常数．若原方程的一个根大于 $3$，另一个根小于 $3$，求 $k$ 的最大整数值．
【难度】
【出处】
无
【标注】
【答案】
$k$ 的最大整数值为 $2$
【解析】
判别式 $\Delta=(k-5)^2-4(1-k)=(k-3)^2+12>0$，
即原方程始终有两个不相等的实数根．
由题意可得二次函数 $y=x^2+(k-5)x+1-k$ 的图象如图所示：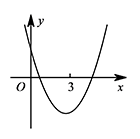
故当 $x=3$ 时，$y<0$．
所以 $9+3(k-5)+1-k<0$，解得 $k<\dfrac 52$，
即 $k$ 的最大整数值为 $2$．
即原方程始终有两个不相等的实数根．
由题意可得二次函数 $y=x^2+(k-5)x+1-k$ 的图象如图所示：
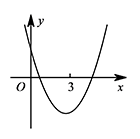故当 $x=3$ 时，$y<0$．所以 $9+3(k-5)+1-k<0$，解得 $k<\dfrac 52$，
即 $k$ 的最大整数值为 $2$．
答案
解析
备注
