在平面直角坐标系 $xOy$ 中，直线 $l_1:y=k_1x+b$ 过 $A(0,-3),B(5,2)$ 两点，直线 $l_2:y=k_2x+2$．当 $x\geqslant 4$ 时，不等式 $k_1x+b>k_2x+2$ 恒成立，求 $k_2$ 的取值范围．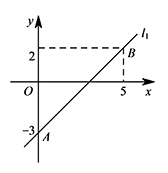
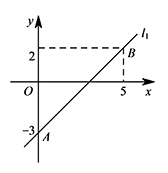
【难度】
【出处】
无
【标注】
【答案】
$k_2$ 的取值范围为 $k_2<-\dfrac 14$
【解析】
因为直线 $l_1:y=k_1x+b$ 经过 $A(0,-3),B(5,2)$ 两点，
所以 $\begin{cases}b=-3,\\ 5k_1+b=2.\end{cases}$
解得 $\begin{cases}k_1=1,\\ b=-3.\end{cases}$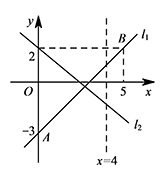
如图所示，若当 $x\geqslant 4$ 时，不等式 $k_1x+b>k_2x+2$ 恒成立，
则当 $x=4$ 时，有 $4k_1+b>4k_2+2$，
即 $4-3>4k_2+2$，
解得 $k_2<-\dfrac 14$．
综上可得，满足题意的 $k_2$ 的取值范围为 $k_2<-\dfrac 14$．
所以 $\begin{cases}b=-3,\\ 5k_1+b=2.\end{cases}$
解得 $\begin{cases}k_1=1,\\ b=-3.\end{cases}$
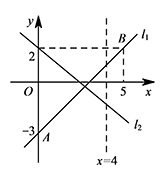如图所示，若当 $x\geqslant 4$ 时，不等式 $k_1x+b>k_2x+2$ 恒成立，则当 $x=4$ 时，有 $4k_1+b>4k_2+2$，
即 $4-3>4k_2+2$，
解得 $k_2<-\dfrac 14$．
综上可得，满足题意的 $k_2$ 的取值范围为 $k_2<-\dfrac 14$．
答案
解析
备注
