如图，$\triangle AOB$ 的顶点 $A,B$ 分别在 $x,y$ 轴上，$\angle BAO=45^\circ$，且 $\triangle AOB$ 的面积为 $8$．过点 $A,B$ 的抛物线 $G$ 向下平移 $4$ 个单位后，恰好与直线 $AB$ 只有一个交点 $N$，求点 $N$ 的坐标．
【难度】
【出处】
无
【标注】
【答案】
点 $N$ 的坐标为 $(2,2)$
【解析】
由 $\angle BAO=45^\circ$，可得 $OA=OB$．
而 $S_{\triangle AOB}=\dfrac 12 OA\cdot OB=8$，所以 $OA=OB=4$，
所以点 $A(4,0)$，点 $B(0,4)$，
则直线 $AB$ 为 $y=-x+4$．
由题意可知抛物线 $G$ 开口向下，设其解析式为 $y=ax^2+bx+c(a<0)$．
则有 $\begin{cases}16a+4b+c=0,\\ c=4,\end{cases}$
从而 $b=-4a-1$．
所以抛物线 $G$ 为 $y=ax^2-(4a+1)x+4$．
将其向下平移 $4$ 个单位后得到抛物线 $G'$ 为 $y=ax^2-(4a+1)x$．
联立方程组 $\begin{cases}y=ax^2-(4a+1)x,\\y=-x+4.\end{cases}$
即 $ax^2-4ax-4=0$．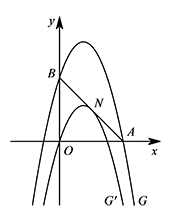
如图，因为抛物线 $G'$ 与直线 $AB$ 只有一个交点，
所以 $\Delta=16a^2+16a=16a(a+1)=0$，即 $a=-1$．
从而 $-x^2+4x-4=0$，解得 $x=2$．
所以点 $N$ 的坐标为 $(2,2)$．
而 $S_{\triangle AOB}=\dfrac 12 OA\cdot OB=8$，所以 $OA=OB=4$，
所以点 $A(4,0)$，点 $B(0,4)$，
则直线 $AB$ 为 $y=-x+4$．
由题意可知抛物线 $G$ 开口向下，设其解析式为 $y=ax^2+bx+c(a<0)$．
则有 $\begin{cases}16a+4b+c=0,\\ c=4,\end{cases}$
从而 $b=-4a-1$．
所以抛物线 $G$ 为 $y=ax^2-(4a+1)x+4$．
将其向下平移 $4$ 个单位后得到抛物线 $G'$ 为 $y=ax^2-(4a+1)x$．
联立方程组 $\begin{cases}y=ax^2-(4a+1)x,\\y=-x+4.\end{cases}$
即 $ax^2-4ax-4=0$．
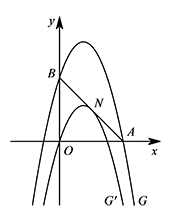如图，因为抛物线 $G'$ 与直线 $AB$ 只有一个交点，所以 $\Delta=16a^2+16a=16a(a+1)=0$，即 $a=-1$．
从而 $-x^2+4x-4=0$，解得 $x=2$．
所以点 $N$ 的坐标为 $(2,2)$．
答案
解析
备注
