已知 $\triangle ABC$ 中 $A,B,C$ 所对的边分别为 $a,b,c$,且 $a+b>2c$,求证:$A+B>2C$.
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
以 $A,B$ 为焦点 $2c$ 为长轴长作椭圆 $E$,则 $C$ 在椭圆 $E$ 外部.设 $AC$ 与椭圆 $E$ 交于点 $C_1$,椭圆 $E$ 的上顶点为 $P$,则\[\angle ACB<\angle AC_1B\leqslant \angle APB=\dfrac{\pi}3,\]因此原命题得证.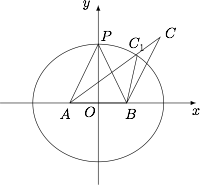

答案
解析
备注