已知函数 $y_1=ax^2+bx,y_2=ax+b$，其中 $ab\ne 0$，在同一平面直角坐标系中，若函数 $y_2$ 的图象经过 $y_1$ 的顶点，当 $1<x<\dfrac 32$ 时，比较 $y_1,y_2$ 的大小．
【难度】
【出处】
无
【标注】
【答案】
当 $a>0$ 时，$y_1<y_2$；当 $a<0$ 时，$y_1>y_2$
【解析】
抛物线 $y_1=ax^2+bx$ 顶点的坐标 $\left(-\dfrac {b}{2a},-\dfrac{b^2}{4a}\right)$，
将其代入代入 $y_2=ax+b$，可得 $b=-2a$．
所以 $y_1-y_2=a(x-2)(x-1)$．
令 $y=a(x-2)(x-1)$，分类讨论 $a$ 的取值：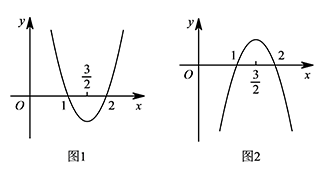
① 当 $a>0$ 时，$y=a(x-2)(x-1)$ 的图象如图1所示．
当 $1<x<\dfrac 32$ 时，$y<0$，即 $y_1<y_2$；
② 当 $a<0$ 时，$y=a(x-2)(x-1)$ 的图象如图2所示．
当 $1<x<\dfrac 32$ 时，$y>0$，即 $y_1>y_2$．
将其代入代入 $y_2=ax+b$，可得 $b=-2a$．
所以 $y_1-y_2=a(x-2)(x-1)$．
令 $y=a(x-2)(x-1)$，分类讨论 $a$ 的取值：
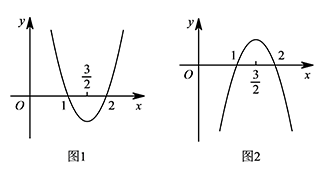① 当 $a>0$ 时，$y=a(x-2)(x-1)$ 的图象如图1所示．当 $1<x<\dfrac 32$ 时，$y<0$，即 $y_1<y_2$；
② 当 $a<0$ 时，$y=a(x-2)(x-1)$ 的图象如图2所示．
当 $1<x<\dfrac 32$ 时，$y>0$，即 $y_1>y_2$．
答案
解析
备注
