在平面直角坐标系 $xOy$ 中，点 $P\left(n,0\right)$ 是 $x$ 轴上的一个动点，过点 $P$ 作垂直于 $x$ 轴的直线交一次函数 $y=kx+b$ 的图象于点 $M$，交二次函数 $y=x^2-2x-3$ 的图象于点 $N$．若只有当 $-2<n<2$ 时，点 $M$ 位于点 $N$ 的上方，求这个一次函数的解析式．
【难度】
【出处】
无
【标注】
【答案】
一次函数解析式为 $y=-2x+1$
【解析】
依题意并结合图象可知，直线 $y=kx+b$ 与抛物线 $y=x^2-2x-3$ 交点的横坐标分别为 $-2$ 和 $2$，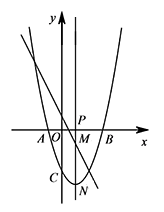
所以两交点的坐标为 $\left(-2,5\right),\left(2,-3\right)$，
将其代入一次函数解析式 $y=kx+b$，得 $\begin{cases}-2k+b=5,\\2k+b=-3.\end{cases}$
解得 $\begin{cases}k=-2,\\b=1.\end{cases}$
所以一次函数解析式为 $y=-2x+1$．
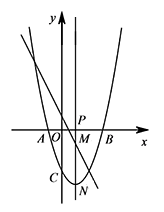所以两交点的坐标为 $\left(-2,5\right),\left(2,-3\right)$，将其代入一次函数解析式 $y=kx+b$，得 $\begin{cases}-2k+b=5,\\2k+b=-3.\end{cases}$
解得 $\begin{cases}k=-2,\\b=1.\end{cases}$
所以一次函数解析式为 $y=-2x+1$．
答案
解析
备注
