在平面直角坐标系 $xOy$ 中，抛物线 $y=x^2-4x+3$ 与 $x$ 轴交于点 $A,B$（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C$．垂直于 $y$ 轴的直线 $l$ 与抛物线交于点 $P(x_1,y_1),Q(x_2,y_2)$，与直线 $BC$ 交于点 $N(x_3,y_3)$，若 $x_1<x_2<x_3$，结合函数的图象，求 $x_1+x_2+x_3$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$7<x_1+x_2+x_3<8$
【解析】
由 $y=x^2-4x+3=(x-1)(x-3)=(x-2)^2-1$，
可得点 $A(1,0)$，点 $B(3,0)$，点 $C(0,3)$，抛物线顶点坐标为 $(2,-1)$．
设直线 $BC$ 的解析式为 $y=kx+b$，
则有 $\begin{cases}3k+b=0,\\b=3,\end{cases}$ 解得 $\begin{cases}k=-1,\\b=3.\end{cases}$
所以直线 $BC$ 的解析式为 $y=-x+3$．
由题意可得 $y_1=y_2$，即 $x_1^2-4x_1+3=x_2^2-4x_2+3$，
整理得 $(x_1-x_2)(x_1+x_2-4)=0$，
所以 $x_1+x_2=4$．
由题意可得，点 $N$ 在 $x$ 轴的下方，如图所示．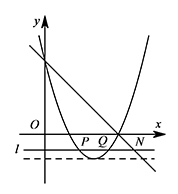
当直线 $l$ 经过抛物线顶点，即 $y_1=y_2=y_3=-1$ 时，$x_3=4$．
结合图象，可得 $3<x_3<4$，
所以 $7<x_1+x_2+x_3<8$．
可得点 $A(1,0)$，点 $B(3,0)$，点 $C(0,3)$，抛物线顶点坐标为 $(2,-1)$．
设直线 $BC$ 的解析式为 $y=kx+b$，
则有 $\begin{cases}3k+b=0,\\b=3,\end{cases}$ 解得 $\begin{cases}k=-1,\\b=3.\end{cases}$
所以直线 $BC$ 的解析式为 $y=-x+3$．
由题意可得 $y_1=y_2$，即 $x_1^2-4x_1+3=x_2^2-4x_2+3$，
整理得 $(x_1-x_2)(x_1+x_2-4)=0$，
所以 $x_1+x_2=4$．
由题意可得，点 $N$ 在 $x$ 轴的下方，如图所示．
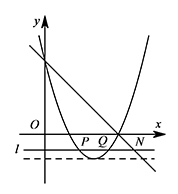当直线 $l$ 经过抛物线顶点，即 $y_1=y_2=y_3=-1$ 时，$x_3=4$．结合图象，可得 $3<x_3<4$，
所以 $7<x_1+x_2+x_3<8$．
答案
解析
备注
