已知抛物线 $y=x^2+(2m+1)x+m(m-3)$（$m$ 为常数，$-1\leqslant m\leqslant 4$），$A(-m-1,y_1)$，$B(\dfrac m2,y_2)$，$C(-m,y_3)$ 是抛物线上不同的三点，将抛物线的对称轴绕坐标原点 $O$ 逆时针旋转 $90^\circ$ 得到直线 $a$，过抛物线顶点 $P$ 作 $PH\perp a$ 于 $H$，当 $1<PH\leqslant 6$ 时，试比较 $y_1,y_2,y_3$ 之间的大小．
【难度】
【出处】
无
【标注】
【答案】
当 $-1\leqslant m<-\dfrac 23$ 或 $\dfrac{5}{12}<m\leqslant \dfrac{25}{12}$ 时，有 $y_2>y_3=y_1$；
当 $-\dfrac 23< m<-\dfrac 14$ 时，有 $y_2<y_3=y_1$
当 $-\dfrac 23< m<-\dfrac 14$ 时，有 $y_2<y_3=y_1$
【解析】
因为顶点坐标为 $(-\dfrac{2m+1}{2},-\dfrac{16m+1}{4})$，
所以 $PH=\left|\dfrac{12m-1}{4}\right|$．
因为 $1<PH\leqslant 6$，$-1\leqslant m\leqslant 4$，
所以当 $\dfrac{12m-1}{4}>0$ 时，解得 $\dfrac{5}{12}<m\leqslant \dfrac{25}{12}$，
所以当 $\dfrac{12m-1}{4}<0$ 时，解得 $-1\leqslant m< -\dfrac{1}{4}$．
因为点 $A(-m-1,y_1)$ 在抛物线上，所以 $y_1=-4m$，
因为点 $C(-m,y_3)$ 在抛物线上，所以 $y_3=-4m$，
所以 $y_1=y_3$．
① 若 $\dfrac m2<-m-1$，则有 $m<-\dfrac 23$．
因为 $-1\leqslant m< -\dfrac{1}{4}$，所以 $-1\leqslant m<-\dfrac 23$．
此时，在对称轴的左侧，$y$ 随 $x$ 的增大而减小，如图：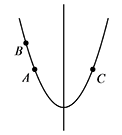
所以 $y_2>y_1=y_3$；
② 若 $\dfrac m2=-m-1$，则点 $A$ 与点 $B$ 重合，此种情况不合题意，故舍去；
③ 若 $\dfrac m2>-m-1$，且 $\dfrac m2\leqslant -\dfrac{2m+1}{2}$ 时，有 $-\dfrac 23<m\leqslant -\dfrac 13$．
因为 $-1\leqslant m< -\dfrac{1}{4}$，所以 $-\dfrac 23<m\leqslant -\dfrac 13$，
此时，在对称轴的左侧，$y$ 随 $x$ 的增大而减小，如图：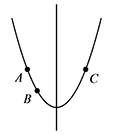
所以 $y_1=y_3>y_2$；
④ 若 $-\dfrac{2m+1}{2}\leqslant \dfrac{m}{2}<-m$，有 $-\dfrac 13\leqslant m<0$．
因为 $-1\leqslant m< -\dfrac{1}{4}$，所以 $-\dfrac 13\leqslant m<-\dfrac 14$，
此时，在对称轴的右侧，$y$ 随 $x$ 的增大而增大，如图：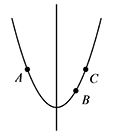
所以 $y_2<y_3=y_1$；
⑤ 若 $\dfrac m2=-m$，则 $B,C$ 重合，不合题意，故舍去；
⑥ 若 $\dfrac m2>-m$，有 $m>0$．
因为 $\dfrac{5}{12}<m\leqslant \dfrac{25}{12}$，所以 $\dfrac{5}{12}<m\leqslant \dfrac{25}{12}$．
此时，在对称轴的右侧，$y$ 随 $x$ 的增大而增大，如图：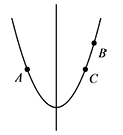
所以 $y_2>y_3=y_1$．
综上所述，当 $-1\leqslant m<-\dfrac 23$ 或 $\dfrac{5}{12}<m\leqslant \dfrac{25}{12}$ 时，有 $y_2>y_3=y_1$；
当 $-\dfrac 23< m<-\dfrac 14$ 时，有 $y_2<y_3=y_1$．
所以 $PH=\left|\dfrac{12m-1}{4}\right|$．
因为 $1<PH\leqslant 6$，$-1\leqslant m\leqslant 4$，
所以当 $\dfrac{12m-1}{4}>0$ 时，解得 $\dfrac{5}{12}<m\leqslant \dfrac{25}{12}$，
所以当 $\dfrac{12m-1}{4}<0$ 时，解得 $-1\leqslant m< -\dfrac{1}{4}$．
因为点 $A(-m-1,y_1)$ 在抛物线上，所以 $y_1=-4m$，
因为点 $C(-m,y_3)$ 在抛物线上，所以 $y_3=-4m$，
所以 $y_1=y_3$．
① 若 $\dfrac m2<-m-1$，则有 $m<-\dfrac 23$．
因为 $-1\leqslant m< -\dfrac{1}{4}$，所以 $-1\leqslant m<-\dfrac 23$．
此时，在对称轴的左侧，$y$ 随 $x$ 的增大而减小，如图：
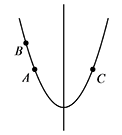所以 $y_2>y_1=y_3$；② 若 $\dfrac m2=-m-1$，则点 $A$ 与点 $B$ 重合，此种情况不合题意，故舍去；
③ 若 $\dfrac m2>-m-1$，且 $\dfrac m2\leqslant -\dfrac{2m+1}{2}$ 时，有 $-\dfrac 23<m\leqslant -\dfrac 13$．
因为 $-1\leqslant m< -\dfrac{1}{4}$，所以 $-\dfrac 23<m\leqslant -\dfrac 13$，
此时，在对称轴的左侧，$y$ 随 $x$ 的增大而减小，如图：
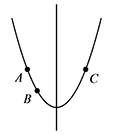所以 $y_1=y_3>y_2$；④ 若 $-\dfrac{2m+1}{2}\leqslant \dfrac{m}{2}<-m$，有 $-\dfrac 13\leqslant m<0$．
因为 $-1\leqslant m< -\dfrac{1}{4}$，所以 $-\dfrac 13\leqslant m<-\dfrac 14$，
此时，在对称轴的右侧，$y$ 随 $x$ 的增大而增大，如图：
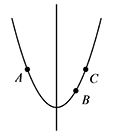所以 $y_2<y_3=y_1$；⑤ 若 $\dfrac m2=-m$，则 $B,C$ 重合，不合题意，故舍去；
⑥ 若 $\dfrac m2>-m$，有 $m>0$．
因为 $\dfrac{5}{12}<m\leqslant \dfrac{25}{12}$，所以 $\dfrac{5}{12}<m\leqslant \dfrac{25}{12}$．
此时，在对称轴的右侧，$y$ 随 $x$ 的增大而增大，如图：
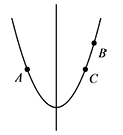所以 $y_2>y_3=y_1$．综上所述，当 $-1\leqslant m<-\dfrac 23$ 或 $\dfrac{5}{12}<m\leqslant \dfrac{25}{12}$ 时，有 $y_2>y_3=y_1$；
当 $-\dfrac 23< m<-\dfrac 14$ 时，有 $y_2<y_3=y_1$．
答案
解析
备注
